题目内容
17.已知函数f(x)=$\sqrt{3}$sinωx-cosωx,x=$\frac{π}{3}$为y=f(x)的对称轴,且f(x)在区间(-$\frac{π}{3}$,$\frac{π}{3}$)单调,则ω=( )| A. | -4 | B. | -1 | C. | 2 | D. | 5 |
分析 利用辅助角公式化简f(x)=$\sqrt{3}$sinωx-cosωx=2sin(ωx$-\frac{π}{6}$),根据x=$\frac{π}{3}$,可得f($\frac{π}{3}$)是最大值或最小值,可得ω的值,在根据f(x)在区间(-$\frac{π}{3}$,$\frac{π}{3}$)单调,确定ω即可.
解答 解:由题意,f(x)=$\sqrt{3}$sinωx-cosωx=2sin(ωx$-\frac{π}{6}$),
∵x=$\frac{π}{3}$为y=f(x)的对称轴,
∴当x=$\frac{π}{3}$时,若f($\frac{π}{3}$)是最大值,
令$\frac{ωπ}{3}$$-\frac{π}{6}$=$\frac{π}{2}$,可得ω=2.
则f(x)=2sin(2x$-\frac{π}{6}$),
考查f(x)在区间(-$\frac{π}{3}$,$\frac{π}{3}$)不是单调函数.
若f($\frac{π}{3}$)是最小值,
令$\frac{ωπ}{3}$$-\frac{π}{6}$=-$\frac{π}{2}$,可得ω=-1.
则f(x)=2sin(-x$-\frac{π}{6}$),
考查f(x)在区间(-$\frac{π}{3}$,$\frac{π}{3}$)是单调函数.
故选B.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
相关题目
7.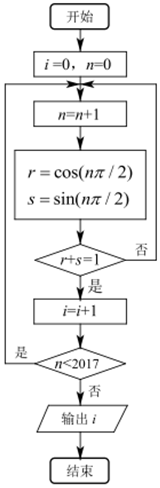 执行如图所示的程序框图,则输出i的值为( )
执行如图所示的程序框图,则输出i的值为( )
 执行如图所示的程序框图,则输出i的值为( )
执行如图所示的程序框图,则输出i的值为( )| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
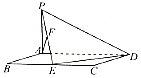 如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.
如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.