��Ŀ����
2����ֱ֪��l��$\left\{{\begin{array}{l}{x=1+tcos��}\\{y=tsin��}\end{array}}$������tΪ��������Ϊ��б�ǣ���������ԭ��OΪ���㣬x���������Ϊ���ᣬ����������ϵ������C�ļ����귽��Ϊ��=$\frac{cos��}{{{{sin}^2}��}}$����1����C��ֱ�����귽�̣�����C�Ľ���F��ֱ�����ꣻ
��2����֪��P��1��0������ֱ��l��C�ཻ��A��B���㣬��$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}$=2�����FAB�������
���� ��1��ԭ���̱���Ϊ��2sin2��=��cos�ȣ����û�����ʽ�ɵã�C��ֱ�����귽�̣�
��2����l�ķ��̴���y2=x��t2sin2��-tcos��-1=0�����ø���ϵ���Ĺ�ϵ������֪�ɵã�|t1-t2|=2|t1t2|��ƽ����${��{{t_1}+{t_2}}��^2}-4{t_1}{t_2}=4t_1^2t_2^2$���ɵ�sin2��=1�����ɵó���
��� �⣺��1��ԭ���̱���Ϊ��2sin2��=��cos�ȣ�
��x=��cos�ȣ�y=��sin�ȣ�
��C��ֱ�����귽��Ϊy2=x���佹��Ϊ$F��{\frac{1}{4}��0}��$��
��2����l�ķ��̴���y2=x��t2sin2��-tcos��-1=0��
��${t_1}+{t_2}=\frac{cos��}{{{{sin}^2}��}}��{t_1}{t_2}=-\frac{1}{{{{sin}^2}��}}$����
$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}=2?|{PA}|+|{PB}|=2|{PA}|•|{PB}|$��
��|t1-t2|=2|t1t2|��
ƽ����${��{{t_1}+{t_2}}��^2}-4{t_1}{t_2}=4t_1^2t_2^2$����
�Ѣٴ���ڵ�$\frac{{{{cos}^2}��}}{{{{sin}^4}��}}+\frac{4}{{{{sin}^2}��}}=\frac{4}{{{{sin}^4}��}}$����sin2��=1��
�ߦ���ֱ��l����б�ǣ���$��=\frac{��}{2}$��
��l����ͨ����Ϊx=1����|AB|=2��
��F��AB�ľ���d=1-$\frac{1}{4}$=$\frac{3}{4}$
���FAB�����ΪS=$\frac{1}{2}$|AB|��d=$\frac{1}{2}��2��\frac{3}{4}$=$\frac{3}{4}$��
���� ������Ҫ���鼫����ϵ��������̵����֪ʶ�������귽����ƽ��ֱ�����귽�̵Ļ�����һԪ���η��̵ĸ���ϵ���Ĺ�ϵ��������������������������������е��⣮

| A�� | $\frac{1}{a}��\frac{1}{b}$ | B�� | a2��ab | C�� | a2��b2 | D�� | $\frac{1}{a-b}��\frac{1}{a}$ |
��������
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
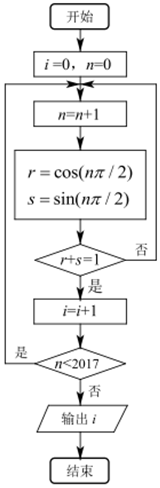 ִ����ͼ��ʾ�ij����ͼ�������i��ֵΪ��������
ִ����ͼ��ʾ�ij����ͼ�������i��ֵΪ��������| A�� | 1006 | B�� | 1007 | C�� | 1008 | D�� | 1009 |
| A�� | a1•d��0 | B�� | |Sn|����Сֵ | ||
| C�� | ${a}_{{n}_{0}}$•${a}_{{n}_{0}+1}$��0 | D�� | ${a}_{{n}_{0}+1}•{a}_{{n}_{0}+2}$��0 |