题目内容

3．变量x，y满足线性约束条件$\left\{\begin{array}{l}{3x+y-2≤0}\\{y-x≤2}\\{y≥-x-1}\end{array}\right.$，目标函数z=kx+y仅在点（0，2）取得最大值，则k的取值范围是（　　）
A．-3＜k＜1B．k＞1C．-1＜k＜1D．-1＜k＜3

分析 由约束条件作出可行域，由题意即可得到k的取值范围．

解答 解：由约束条件$\left\{\begin{array}{l}{3x+y-2≤0}\\{y-x≤2}\\{y≥-x-1}\end{array}\right.$作出可行域如图，

∵目标函数z=kx+y仅在点（0，2）取得最大值，
∴k的取值范围是（-3，1）．
故选：A．

点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．

练习册系列答案
相关题目
13．已知a＜b＜0，则（　　）
A．$\frac{1}{a}＜\frac{1}{b}$B．a2＜abC．a2＜b2D．$\frac{1}{a-b}＜\frac{1}{a}$
14．己知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞1）的左焦点F与抛物线y2=-4x的焦点重合，直线x-y+$\frac{\sqrt{2}}{2}$=0与以原点O为圆心，以椭圆的离心率e为半径的圆相切．
（I ）求该椭圆C的方程
（II）设点P坐标为（-$\frac{1}{8}$，0），若|PA|=|PB|，求直线AB的方程．
11．已知公差为d的等差数列{an}前n项和为Sn，若有确定正整数n0，对任意正整数m，${S}_{{n}_{0}}$•${S}_{{n}_{0}+m}$＜0恒成立，则下列说法错误的是（　　）
A．a1•d＜0B．|Sn|有最小值
C．${a}_{{n}_{0}}$•${a}_{{n}_{0}+1}$＞0D．${a}_{{n}_{0}+1}•{a}_{{n}_{0}+2}$＞0
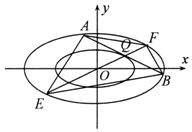18．在直角坐标系xOy中，椭圆C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{2}}}{2}$，左、右焦点分别是F1，F2，P为椭圆C1上任意一点，|PF1|2+|PF2|2的最小值为8．
（I）求椭圆C1的方程；
（II）设椭圆C2：$\frac{{2{x^2}}}{a^2}+\frac{{2{y^2}}}{b^2}=1，Q（{{x_0}，{y_0}}）$为椭圆C2上一点，过点Q的直线交椭圆C1于A，B两点，且Q为线段AB的中点，过O，Q两点的直线交椭圆C1于E，F两点．
（i）求证：直线AB的方程为x0x+2y0y=2；
（ii）当Q在椭圆C2上移动时，四边形AEBF的面积是否为定值？若是，求出该定值；不是，请说明理由．
8．某高中组织数学知识竞赛，采取答题闯关的形式，分两种题型，每种题型设两关．“数学文化”题答对一道得5分，“数学应用”题答对一道得10分，答对一道题即可进入下一关，否则终止比赛．有甲、乙、丙三人前来参赛，设三人答对每道题的概率分别是$\frac{3}{4}$、$\frac{2}{3}$、$\frac{1}{2}$，三人答题互不影响．甲、乙选择“数学文化”题，丙选择“数学应用”题．
（Ⅰ）求乙、丙两人所得分数相等的概率；
（Ⅱ）设甲、丙两人所得分数之和为随机变量X，求X的分布列与期望．
15．执行如图所示程序框图，若输入的k=4，则输出的s=（　　）
A．$\frac{1}{3}$B．$\frac{4}{5}$C．$\frac{5}{6}$D．$\frac{6}{7}$
12．已知椭圆C：$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，点$P（\sqrt{2}，2）$在椭圆上．
（1）求椭圆C的方程；
（2）过椭圆上的焦点F作两条相互垂直的弦AC，BD，求|AC|+|BD|的取值范围．
13．已知向量$\overrightarrow{a}$=（-4，x），$\overrightarrow{b}$=（1，2），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则x=2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网