题目内容
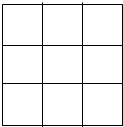 将大小形状相同的4个红球和2个白球放入如图所示的九宫格中,每格至多放一个,要求相邻方格的小球不同色(有公共边的两个方格为相邻),则所有不同的放法种数为( )
将大小形状相同的4个红球和2个白球放入如图所示的九宫格中,每格至多放一个,要求相邻方格的小球不同色(有公共边的两个方格为相邻),则所有不同的放法种数为( )| A、32 | B、48 | C、50 | D、54 |
考点:排列、组合及简单计数问题
专题:排列组合
分析:由题意需要分类,根据红球的位置进行分类,如图所示,分三类,然后根据分类计数原理可得答案.
解答:
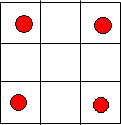
解:第一类,当4个红球在4个顶角的位置时,白球放在除最中间后剩下4个格种任选两个,故有
=6种,如图
第二类,当有一个红球再最中间时,其它三个红球只能放在顶角位置,有
=4种,
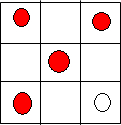
当其中一个白球在顶角时,另一个白球只有2种方法,当白球不在顶角时,白球放在除顶角后剩下4个格种任选两个有
=6种,故有4×(2+6)=32种,如图
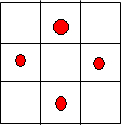
第三类,当4个红球放在每外围三个格的中间时,白球从白球放在剩下5个格种任选两个有
=10种,如图
根据分类计数原理,故有6+32+10=48.
故选:B
| C | 2 4 |

第二类,当有一个红球再最中间时,其它三个红球只能放在顶角位置,有
| C | 3 4 |
当其中一个白球在顶角时,另一个白球只有2种方法,当白球不在顶角时,白球放在除顶角后剩下4个格种任选两个有
| C | 2 4 |

第三类,当4个红球放在每外围三个格的中间时,白球从白球放在剩下5个格种任选两个有
| C | 2 5 |

根据分类计数原理,故有6+32+10=48.
故选:B
点评:本题主要考查了分类计数原理,关键是如何分类,属于中档题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
从正六边形六个顶点及其中心这7个点中,任取两个点,则这两个点的距离大于该正六边形边长的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 在正方形ABCD-A1B1C1D1中,G,H分别是B1C1,C1D1的中点.
在正方形ABCD-A1B1C1D1中,G,H分别是B1C1,C1D1的中点.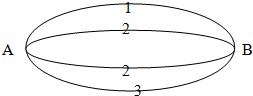 如图A、B两点之间有4条网线并联,他们能通过的最大信息量分别为1、2、2、3,现从中任取三条网线且使每条网线通过最大信息量;
如图A、B两点之间有4条网线并联,他们能通过的最大信息量分别为1、2、2、3,现从中任取三条网线且使每条网线通过最大信息量;