题目内容
设an=3n,求证:
<
+
+…+
<1.
1-(
| ||
| 2 |
| 1 |
| a1-1 |
| 1 |
| a2-1 |
| 1 |
| an-1 |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:
=
>
,
=
<
,利用放缩法即可得证.
| 1 |
| an-1 |
| 1 |
| 3n-1 |
| 1 |
| 3n |
| 1 |
| an-1 |
| 1 |
| 3n-1 |
| 1 |
| 2n |
解答:
证明:∵an=3n,
∴
=
>
,
∴
+
+…+
>
+
+…+
=
=
,
又∵
=
<
,
∴
+
+…+
<
+
+…+
=
=1-
<1,
∴
<
+
+…+
<1.
∴
| 1 |
| an-1 |
| 1 |
| 3n-1 |
| 1 |
| 3n |
∴
| 1 |
| a1-1 |
| 1 |
| a2-1 |
| 1 |
| an-1 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
| ||||
1-
|
1-(
| ||
| 2 |
又∵
| 1 |
| an-1 |
| 1 |
| 3n-1 |
| 1 |
| 2n |
∴
| 1 |
| a1-1 |
| 1 |
| a2-1 |
| 1 |
| an-1 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| ||||
1-
|
| 1 |
| 2n |
∴
1-(
| ||
| 2 |
| 1 |
| a1-1 |
| 1 |
| a2-1 |
| 1 |
| an-1 |
点评:本题主要考查利用放缩法证明不等式问题,放缩后利用等比数列求和公式计算,考查学生的逻辑思维能力及运算求解能力,属于难题.

练习册系列答案
相关题目
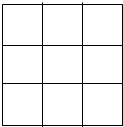 将大小形状相同的4个红球和2个白球放入如图所示的九宫格中,每格至多放一个,要求相邻方格的小球不同色(有公共边的两个方格为相邻),则所有不同的放法种数为( )
将大小形状相同的4个红球和2个白球放入如图所示的九宫格中,每格至多放一个,要求相邻方格的小球不同色(有公共边的两个方格为相邻),则所有不同的放法种数为( )