题目内容
设正实数a,b满足a+2b=2.则ab的最大值为 :a2+b2的最小值为 .
考点:基本不等式
专题:不等式的解法及应用
分析:由题意可得2=a+2b≥2
,变形可得ab的最大值;又可得a=2-2b且0<b<1,代入a2+b2由二次函数区间的最值可得.
| a•2b |
解答:
解:∵正实数a,b满足a+2b=2,
∴2=a+2b≥2
,
∴
≤1,∴ab≤
当且即当a=2b时取等号;
由正实数a,b满足a+2b=2可得a=2-2b,
再由a=2-2b>0可得b<1,即0<b<1,
∴a2+b2=(2-2b)2+b2=5b2-8b+4,
由二次函数可知当b=-
=
时,a2+b2取最小值
故答案为:
;
∴2=a+2b≥2
| a•2b |
∴
| 2ab |
| 1 |
| 2 |
当且即当a=2b时取等号;
由正实数a,b满足a+2b=2可得a=2-2b,
再由a=2-2b>0可得b<1,即0<b<1,
∴a2+b2=(2-2b)2+b2=5b2-8b+4,
由二次函数可知当b=-
| -8 |
| 2×5 |
| 4 |
| 5 |
| 4 |
| 5 |
故答案为:
| 1 |
| 2 |
| 4 |
| 5 |
点评:本题考查基本不等式求最值,涉及二次函数区间的最值,属中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
已知sin(π+α)=
,α为第三象限角,则tanα=( )
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知数列{an}满足an=17-3n,则使其前n项的和Sn取最大值时n的值为( )
| A、4 | B、5 | C、6 | D、7 |
已知定义在R上的凼数y=f(x)满足f(x+A+B)=f(x),其中A,B分别是函数g(x)=
的最大值和最小值,若当0≤x≤1时,f(x)=(
)x,则f(2015)=( )
| |x|+sinx+1 |
| |x|+1 |
| 1 |
| 2 |
| A、1 | ||
| B、0 | ||
C、-
| ||
D、
|
执行如图所示的算法,则输出的结果是( )


| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
若不等式x2-px+q=0的解集为(-
,
),则不等式qx2+px+1>0的解集为( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、(-3,2) | ||||
| B、(-2,3) | ||||
C、(-
| ||||
D、(-
|
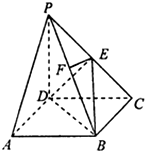 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB,垂足为F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB,垂足为F.