题目内容
设双曲线C的中心在原点,以点A(
,0)为右焦点,以x=
为右准线.
(1)求双曲线C的方程;
(2)设直线l:y=kx+1与双曲线交于A、B两点,若以A、B为直径的圆经过原点,求k的值.
| 2 |
| 3 |
| 3 |
| ||
| 6 |
(1)求双曲线C的方程;
(2)设直线l:y=kx+1与双曲线交于A、B两点,若以A、B为直径的圆经过原点,求k的值.
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)设双曲线的方程为
-
=1,依题意,由其焦点坐标与准线方程可求得a2=
,b2=1,从而可得双曲线C的方程;
(2)联立直线y=kx+1与双曲线3x2-y2=1可得(3-k2)x2-2kx-2=0,设A(x1,y1)、B(x2,y2),依题意,x1x2+y1y2=0,利用韦达定理可得又x1+x2=
,x1x2=
,从而可求得
+1=0,继而可解得k的值.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
(2)联立直线y=kx+1与双曲线3x2-y2=1可得(3-k2)x2-2kx-2=0,设A(x1,y1)、B(x2,y2),依题意,x1x2+y1y2=0,利用韦达定理可得又x1+x2=
| -2k |
| k2-3 |
| 2 |
| k2-3 |
| 2 |
| k2-3 |
解答:
解:(1)设双曲线的方程为
-
=1,
由焦点坐标得c=
,
准线方程x=±
,即有a2=
×
=
,
∵c2=a2+b2,
∴b2=1,
∴双曲线C的方程为:3x2-y2=1;
(2)由
得(3-k2)x2-2kx-2=0,
由△>0,且3-k2≠0,得-
<k<
,且k≠±
.
设A(x1,y1)、B(x2,y2),
因为以AB为直径的圆过原点,所以OA⊥OB,
所以 x1x2+y1y2=0,又x1+x2=
,x1x2=
,
∴y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1,
∴k2x1x2+k(x1+x2)+1+x1x2=0,
即
+
+1+
=0,
∴
+1=0,解得k=±1.
| x2 |
| a2 |
| y2 |
| b2 |
由焦点坐标得c=
2
| ||
| 3 |
准线方程x=±
| a2 |
| c |
| ||
| 6 |
2
| ||
| 3 |
| 1 |
| 3 |
∵c2=a2+b2,
∴b2=1,
∴双曲线C的方程为:3x2-y2=1;
(2)由
|
由△>0,且3-k2≠0,得-
| 6 |
| 6 |
| 3 |
设A(x1,y1)、B(x2,y2),
因为以AB为直径的圆过原点,所以OA⊥OB,
所以 x1x2+y1y2=0,又x1+x2=
| -2k |
| k2-3 |
| 2 |
| k2-3 |
∴y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1,
∴k2x1x2+k(x1+x2)+1+x1x2=0,
即
| 2k2 |
| k2-3 |
| -2k2 |
| k2-3 |
| 2 |
| k2-3 |
∴
| 2 |
| k2-3 |
点评:本题考查双曲线的标准方程和性质,着重考查直线与圆锥曲线的位置关系,突出考查韦达定理的应用,考查转化思想与综合运算能力,属于中档题.

练习册系列答案
相关题目
若命题p:2n-1(n∈Z)是奇数;q:2n+1(n∈Z)是偶数,则下列说法中正确的是( )
| A、¬p为真 | B、¬q为假 |
| C、p∨q为真 | D、p∧q为真 |
 四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点
四棱锥P-ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点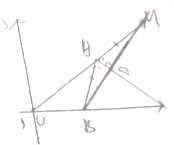 如图,△ABC的周长为8,C(0,0),B(2,0),过B的直线与∠CAB的外角平分线垂直,且交AC的延长线于M,求点M的轨迹方程.
如图,△ABC的周长为8,C(0,0),B(2,0),过B的直线与∠CAB的外角平分线垂直,且交AC的延长线于M,求点M的轨迹方程.
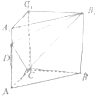 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,四边形BCC1B1是边长为4的正方形,直线AB与平面ACC1A1所成角的正切值为2,点D为棱AA1上的动点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,四边形BCC1B1是边长为4的正方形,直线AB与平面ACC1A1所成角的正切值为2,点D为棱AA1上的动点.