题目内容
若函数y=f(x)(x∈R)满足f(x+2)=f(x)且x∈(-1,1]时,f(x)=1-x2,函数g(x)=
,则函数h(x)=f(x)-g(x)在区间[-5,9]内的零点的个数为 个.
|
考点:函数零点的判定定理,函数的周期性
专题:函数的性质及应用
分析:根据题意,∴f(x)的周期为2,g(x)是关于y轴对称的函数;在同一坐标系中画出函数f(x)、g(x)的图象,
结合图象,得出在区间[-5,9]内两图象交点的个数,即是函数h(x)=f(x)-g(x)在区间[-5,9]内的零点数.
结合图象,得出在区间[-5,9]内两图象交点的个数,即是函数h(x)=f(x)-g(x)在区间[-5,9]内的零点数.
解答:
解:∵f(x+2)=f(x),∴f(x)的周期为2;
又x∈(-1,1]时,f(x)=1-x2,
函数g(x)=
,是关于y轴对称的函数;
在同一坐标系中画出函数f(x)、g(x)的图象,如图所示;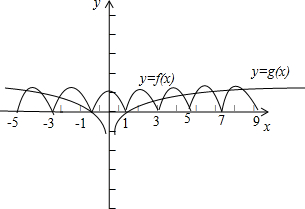
在区间[-5,9]内两图象交点的个数是13,
∴函数h(x)=f(x)-g(x)在区间[-5,9]内的零点的个数为13.
故答案为:13.
又x∈(-1,1]时,f(x)=1-x2,
函数g(x)=
|
在同一坐标系中画出函数f(x)、g(x)的图象,如图所示;

在区间[-5,9]内两图象交点的个数是13,
∴函数h(x)=f(x)-g(x)在区间[-5,9]内的零点的个数为13.
故答案为:13.
点评:本题考查了利用函数的图象判定函数零点的问题,解题时应画出函数图象,根据图象交点的个数来判定函数零点的个数,是中档题.

练习册系列答案
相关题目
半径为R的球的内接正三棱柱的三个侧面积之和的最大值为( )
A、3
| ||
B、
| ||
C、2
| ||
D、
|
已知函数f(x)=
-cosx,若
<a<b<
,则( )
| 1 |
| 2x |
| π |
| 3 |
| 5π |
| 6 |
| A、f(a)>f(b) |
| B、f(a)<f(b) |
| C、f(a)=f(b) |
| D、f(a)f(b)>0 |
已知正三角形ABC的边长是3,D是BC上的点,BD=1,则
•
=( )
| AD |
| BC |
A、-
| ||
B、-
| ||
C、
| ||
D、
|