题目内容
已知y=f(x)在R上的图象是一条连贯的曲线,且对于?∈R,f′(x)均存在,当x≠0时,f′(x)+
>0,则关于x的函数g(x)=f(x)+
的零点的个数为 .
| f(x) |
| x |
| 1 |
| x |
考点:利用导数研究函数的单调性,导数的运算
专题:导数的综合应用
分析:将求g(x)的零点个数转化为求xg(x)的最值问题,由已知求出h(x)=xg(x)>0,得出g(x)>0恒成立.
解答:
解:∵当x≠0时,f′(x)+
>0,
即
>0
令h(x)=xf(x)+1,
∴h′(x)=f(x)+xf′(x),
∴x>0时,h(x)单调递增,
x<0时,h(x)单调递减,
∴h(x)min=h(0)=1>0,
∴x≠0时,g(x)>0恒成立,
故零点的个数是0个,
故答案为:0
| f(x) |
| x |
即
| xf′(x)+f(x) |
| x2 |
令h(x)=xf(x)+1,
∴h′(x)=f(x)+xf′(x),
∴x>0时,h(x)单调递增,
x<0时,h(x)单调递减,
∴h(x)min=h(0)=1>0,
∴x≠0时,g(x)>0恒成立,
故零点的个数是0个,
故答案为:0
点评:本题考查了函数的零点问题,渗透了转化思想,导数问题,函数的单调性问题,构造函数是解决本题的关键.

练习册系列答案
相关题目
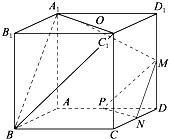 如图,在正方体ABCD-A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点.