题目内容
设a1,d为实数,首项为a1,公差为d的等差数{an}的前n项和为Sn,满足S5S6+15=0.
(Ⅰ)当S5=5时,若bn=|an|,求bn前n项和Tn
(Ⅱ)求d的取值范围.
(Ⅰ)当S5=5时,若bn=|an|,求bn前n项和Tn
(Ⅱ)求d的取值范围.
考点:数列的求和
专题:等差数列与等比数列
分析:(I)根据附加条件,先求得s6再求得a6分别用a1和d表示,再解关于a1和d的方程组.
(II)所求问题是d的范围,所以用“a1,d”法.
(II)所求问题是d的范围,所以用“a1,d”法.
解答:
解:(Ⅰ)由S5=5和S5S6+15=0得S6=-3.∴a6=S6-S5=-8.(1分)∴
.
解得a1=7,d=-3,∴an=10-3n.
由10-3n≥0得n≤
,
∴当n≤3时,Tn=b1+b2+…+bn=|a1|+|a2|+…+|an|=-
n2+
n,
当n≥4时,Tn=b1+b2+…+bn=|a1|+|a2|+…+|an|=
n2-
n+24,
综上Tn=
.
(Ⅱ)因为S5S6+15=0,
所以(5a1+10d)(6a1+15d)+15=0,
整理得
+
a1d+5d2+
=0,
即(a1+
)2=
-
,
∵(a1+
)2≥0,∴
-
≥0,
解得d≤-2
或d≥2
,
∴d的取值范围为(-∞,-2
]∪[2
,+∞).
|
解得a1=7,d=-3,∴an=10-3n.
由10-3n≥0得n≤
| 10 |
| 3 |
∴当n≤3时,Tn=b1+b2+…+bn=|a1|+|a2|+…+|an|=-
| 3 |
| 2 |
| 17 |
| 2 |
当n≥4时,Tn=b1+b2+…+bn=|a1|+|a2|+…+|an|=
| 3 |
| 2 |
| 17 |
| 2 |
综上Tn=
|
(Ⅱ)因为S5S6+15=0,
所以(5a1+10d)(6a1+15d)+15=0,
整理得
| a | 2 1 |
| 9 |
| 2 |
| 1 |
| 2 |
即(a1+
| 9d |
| 4 |
| d2 |
| 16 |
| 1 |
| 2 |
∵(a1+
| 9d |
| 4 |
| d2 |
| 16 |
| 1 |
| 2 |
解得d≤-2
| 2 |
| 2 |
∴d的取值范围为(-∞,-2
| 2 |
| 2 |
点评:本题主要考查等差数列概念、求和公式通项公式等基础知识,同时考查运算求解能力及分析问题解决问题的能力.

练习册系列答案
相关题目
P是椭圆
+
=1上一点,F1,F2分别为左、右焦点,△PF1F2的内切圆的半径为1,则|
+
|的值为( )
| x2 |
| 25 |
| y2 |
| 9 |
| PF1 |
| PF2 |
| A、8 | ||||
B、4
| ||||
| C、4 | ||||
D、
|
已知f(x)=x3+x2f′(1),则f′(2)=( )
| A、0 | B、1 | C、2 | D、3 |
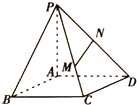 如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥面ABCD,M、N分别为PC,PD上的点,且PM:MC=2:1,N为PD的中点,则满足
如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥面ABCD,M、N分别为PC,PD上的点,且PM:MC=2:1,N为PD的中点,则满足