题目内容
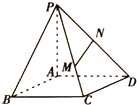 如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥面ABCD,M、N分别为PC,PD上的点,且PM:MC=2:1,N为PD的中点,则满足
如图所示,已知矩形ABCD,P为平面ABCD外一点,且PA⊥面ABCD,M、N分别为PC,PD上的点,且PM:MC=2:1,N为PD的中点,则满足| MN |
| AB |
| AD |
| AP |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:分别以AB,AD,AP,为x,y,z轴,建立空间直角坐标系,不妨令B=(a,0,0),D=(0,b,0),P=(0,0,C),分别表示出M,N的坐标,从而表示出
,得出答案.
| MN |
解答:
解:分别以AB,AD,AP,为x,y,z轴,建立空间直角坐标系,
不妨令B=(a,0,0),D=(0,b,0),P=(0,0,C),
∴M=(
a,
b,
c),N=(0,
b,
c),
∴
=(-
a,-
b,
c),
故答案为:-
,-
,
.
不妨令B=(a,0,0),D=(0,b,0),P=(0,0,C),
∴M=(
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| MN |
| 2 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
故答案为:-
| 2 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
点评:本题考查了平面向量的基本定理及其意义,考查数形结合思想,是一道基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
如图甲所示,在正方形ABCD中,EF分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为H,如图乙所示,那么,在四面体A-EFH中必有( )
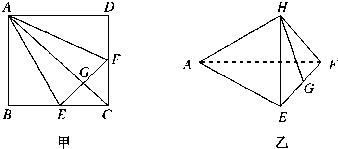

| A、AH⊥△EFH所在平面 |
| B、AG⊥△EFH所在平面 |
| C、HF⊥△AEF所在平面 |
| D、HG⊥△AEF所在平面 |
对任意实数x,<x>表示不小于x的最小整数,如<1.1>=2,<-1.1>=-1,则“|x-y|<1”是“<x>=<y>”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充分 |
| D、既不充分又不必要 |
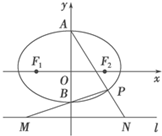 如图,椭圆
如图,椭圆