题目内容
某房地产开发商在销售一幢23层的商品楼之前按下列方法确定房价:由于首层均为复式结构,因此首层价格为a1元/m2,顶层由于景观好价格为a2元/m2,第二层价格为a元/m2,从第三层开始每层在前一层价格上加价
元/m2,则该商品房各层的平均价格为 .
| a |
| 100 |
考点:函数模型的选择与应用
专题:应用题,等差数列与等比数列
分析:利用等差数列的求和公式求出第2层至第22层的价格和,然后由首层的价格、顶层的价格及第2层至第22层的价格和作和后除以23得答案.
解答:
解:首层价格为a1元/m2,顶层价格为a2元/m2,
又第2层价格为a元/m2,从第三层开始每层在前一层价格上加价
元/m2,
则第2层至第22层构成以a为首项,以
为公差的等差数列,
第2层至第22层的价格和为21a+
×
=23.1a.
∴该商品房各层的平均价格为
元/m2.
故答案为:
元/m2.
又第2层价格为a元/m2,从第三层开始每层在前一层价格上加价
| a |
| 100 |
则第2层至第22层构成以a为首项,以
| a |
| 100 |
第2层至第22层的价格和为21a+
| 21×20 |
| 2 |
| a |
| 100 |
∴该商品房各层的平均价格为
| (a1+a2+23.1a) |
| 23 |
故答案为:
| (a1+a2+23.1a) |
| 23 |
点评:本题考查了函数模型的选择与应用,考查了等差数列的前n项和,是基础题.

练习册系列答案
相关题目
已知a>0,若不等式|x-a|+3x≤0的解集为{x|x≤-1},则a的值为( )
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
函数y=
+
是( )
| 1-x2 |
| 2 |
| 1+|x| |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
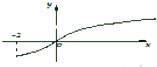 已知f(x)的定义域为[-2,+∞),部分对应值如下表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图,若f(x)<1,则x的范围为
已知f(x)的定义域为[-2,+∞),部分对应值如下表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图,若f(x)<1,则x的范围为