题目内容
已知α,β是两个不同的平面,m,n是直线,下列命题中不正确的是( )
| A、若m⊥α,n⊥α,则m∥n |
| B、若m∥α,n∥α,则m∥n |
| C、若m⊥α,m⊥β,则α∥β |
| D、若m⊥α,m?β,则α⊥β |
考点:平面与平面之间的位置关系,空间中直线与直线之间的位置关系,空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用直线与平面垂直的性质判断选项,利用反例判断错误选项即可.
解答:
解:因为垂直同一个平面的两条直线平行,所以A正确;
m∥α,n∥α,则m∥n,显然不正确,因为mn可能相交也可能异面,所以B不正确.
垂直同一条直线的两个平面平行,所以C正确;
若m⊥α,m?β,则α⊥β,满足平面与平面垂直的二面角的定义,所以D正确.
故选:B.
m∥α,n∥α,则m∥n,显然不正确,因为mn可能相交也可能异面,所以B不正确.
垂直同一条直线的两个平面平行,所以C正确;
若m⊥α,m?β,则α⊥β,满足平面与平面垂直的二面角的定义,所以D正确.
故选:B.
点评:本题考查直线与平面,直线与直线,平面与平面的位置关系的判断,基本知识的考查.

练习册系列答案
相关题目
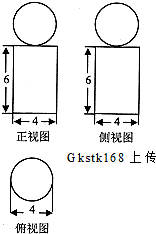 如图是一个空间几何体的三视图(注:正视图也称主视图,侧视图也称左视图),其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成,俯视图是直径等于4的圆,该几何体的体积是( )
如图是一个空间几何体的三视图(注:正视图也称主视图,侧视图也称左视图),其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成,俯视图是直径等于4的圆,该几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
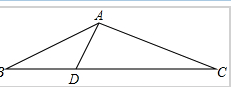 如图△ABC中,∠BAC=120°,AB=1,AC=2,D在BC上,且DC=4BD,则AD的长为
如图△ABC中,∠BAC=120°,AB=1,AC=2,D在BC上,且DC=4BD,则AD的长为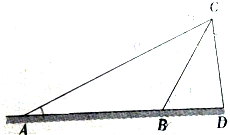 为了测量一个塔的高度,某人站在A处测得塔尖C的仰角为30°,前进100m后达到B处,测得塔尖的仰角为75°,则该塔的高度为
为了测量一个塔的高度,某人站在A处测得塔尖C的仰角为30°,前进100m后达到B处,测得塔尖的仰角为75°,则该塔的高度为