题目内容

求函数y=
tan(
x
2
+
π
3
)
的周期和单调区间．
考点：正切函数的图象
专题：计算题,三角函数的图像与性质
分析：利用正切函数的周期和单调区间，可得结论．
解答： 解：周期T=
π
1
2
=2π，
由tan（
x
2
+
π
3
）≥0，可得kπ≤
x
2
+
π
3
＜kπ+
π
2
，即2kπ-
2π
3
≤x＜2kπ+
π
3
，
利用正切函数的单调区间可得函数y=
tan(
x
2
+
π
3
)
的单调增区间为[2kπ-
2π
3
，2kπ+
π
3
）（k∈Z）．
点评：本题考查函数的周期和单调区间，正确运用正切函数的周期和单调区间是关键．
练习册系列答案
相关题目
已知函数f（x）=2sinωx，其中ω＞0，若x1∈[-
2
3
π，0），x2∈（0，
π
4
]，f（x1）=f（x2），则ω的最小值为
 
．
把函数y=sin（2x-
π
6
）的图象向左平移
π
6
个单位后，所得函数图象的一条对称轴为（　　）
A、x=0
B、x=
π
6
C、x=-
π
12
D、x=
π
2
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的两个焦点F1，F2，点P在椭圆上，则△PF1F2的面积最大值是
 
．
已知首项不为零的数列{an}中的三项a1，a2，a5依次成等比数列，且点（an+1，an）在函数y=
x
1-2x
的图象上．
（1）证明：数列{
1
an
}是等差数列，并求出an；
（2）设bn=anan+1，数列{bn}的前n项和为Sn，求使Sn＜
4
17
成立的最大正整数n的值．
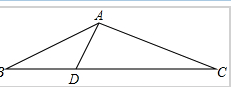如图△ABC中，∠BAC=120°，AB=1，AC=2，D在BC上，且DC=4BD，则AD的长为
 
．
设O是△ABC内一点，且
OA
=
a
，
OB
=
b
，
OC
=
c
，若以线段OA，OB为邻边作平行四边形，第四个顶点为D，再以OC，OD为邻边作平行四边形，其第四个顶点为H，试用
a
，
b
，
c
表示
DC
，
OH
，
BH
．
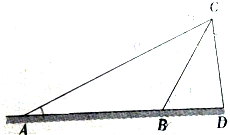为了测量一个塔的高度，某人站在A处测得塔尖C的仰角为30°，前进100m后达到B处，测得塔尖的仰角为75°，则该塔的高度为
 
．
若f（tanx）=sinxcosx，则f（
2
3
）的值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网