题目内容
设f（x2+1）=loga（4-x4）（a＞1），则f（x）的值域是 ．
考点：函数的值域,函数解析式的求解及常用方法
专题：函数的性质及应用
分析：由已知求出函数f（x）的解析式，然后由复合函数值域的求解得答案．
解答：
解：由f（x2+1）=loga（4-x4）（a＞1），
令x2+1=t（t≥1），则x2=t-1，
∴f(t)=loga[4-(t-1)2]=loga(-t2+2t+3)．
则f(x)=loga(-x2+2x+3)（x≥1），
∵x≥1，0＜-x2+2x+3≤4，
则a＞1时函数f（x）的值域是（-∞，2loga2]．
故答案为：（-∞，2loga2]．
令x2+1=t（t≥1），则x2=t-1，
∴f(t)=loga[4-(t-1)2]=loga(-t2+2t+3)．
则f(x)=loga(-x2+2x+3)（x≥1），
∵x≥1，0＜-x2+2x+3≤4，
则a＞1时函数f（x）的值域是（-∞，2loga2]．
故答案为：（-∞，2loga2]．
点评：本题考查了函数解析式的求解及常用方法，考查了函数值域的求法，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
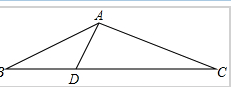如图△ABC中，∠BAC=120°，AB=1，AC=2，D在BC上，且DC=4BD，则AD的长为