题目内容
已知函数f(x)=
sin(ωx+φ+
)对任意的实数x,有f(-x)=f(x),则tanφ的值为( )
| 2 |
| π |
| 4 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
考点:y=Asin(ωx+φ)中参数的物理意义
专题:三角函数的求值
分析:利用已知条件判断函数的奇偶性,求出φ的值,然后求解tanφ的值.
解答:
解:函数f(x)=
sin(ωx+φ+
)对任意的实数x,有f(-x)=f(x),
所以函数是偶函数,则φ+
=kπ+
,k∈Z.
则φ=kπ+
,k∈Z.
tanφ=tan(kπ+
)=tan
=1.
故选:A.
| 2 |
| π |
| 4 |
所以函数是偶函数,则φ+
| π |
| 4 |
| π |
| 2 |
则φ=kπ+
| π |
| 4 |
tanφ=tan(kπ+
| π |
| 4 |
| π |
| 4 |
故选:A.
点评:本题考查三角函数的奇偶性的判断,三角函数的化简求值,考查计算能力.

练习册系列答案
相关题目
抛掷两枚质地均匀的骰子,向上的点数之差的绝对值为3的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
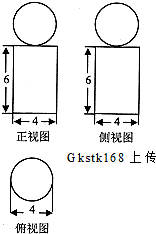 如图是一个空间几何体的三视图(注:正视图也称主视图,侧视图也称左视图),其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成,俯视图是直径等于4的圆,该几何体的体积是( )
如图是一个空间几何体的三视图(注:正视图也称主视图,侧视图也称左视图),其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成,俯视图是直径等于4的圆,该几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
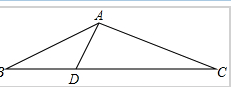 如图△ABC中,∠BAC=120°,AB=1,AC=2,D在BC上,且DC=4BD,则AD的长为
如图△ABC中,∠BAC=120°,AB=1,AC=2,D在BC上,且DC=4BD,则AD的长为 某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下: