题目内容
函数y=ln(2x+3)+x2的单调区间是 .
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求出函数的定义域和导数,利用f′(x)符号,解不等式,即可得到函数的单调区间.
解答:
解:由2x+3>0,可得函数的定义域为(-
,+∞),
则函数的导数为f′(x)=2x+
=2×
,
由f′(x)<0得2x2+3x+1<0,
解得-1<x<-
,
即函数的单调递减区间(-1,-
),
由f′(x)>0得2x2+3x+1>0,
解得-
<x<-1或x>-
,
函数的增区间为(-
,-1),(-
,+∞).
故答案为:函数的单调递减区间(-1,-
);函数的增区间为(-
,-1),(-
,+∞).
| 3 |
| 2 |
则函数的导数为f′(x)=2x+
| 2 |
| 2x+3 |
| 2x2+3x+1 |
| 2x+3 |
由f′(x)<0得2x2+3x+1<0,
解得-1<x<-
| 1 |
| 2 |
即函数的单调递减区间(-1,-
| 1 |
| 2 |
由f′(x)>0得2x2+3x+1>0,
解得-
| 3 |
| 2 |
| 1 |
| 2 |
函数的增区间为(-
| 3 |
| 2 |
| 1 |
| 2 |
故答案为:函数的单调递减区间(-1,-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查函数单调区间的求解,求函数的导数解导数不等式是解决本题的关键.

练习册系列答案
相关题目
设a=
,b=sin85°-
cos85°,c=2(sin47°sin66°-sin24°sin43°)则a、b、c的大小关系是( )
| 4tan12.5° |
| 1-tan212.5° |
| 3 |
| A、b>c>a |
| B、a>b>c |
| C、b>a>c |
| D、c>b>a |
抛掷两枚质地均匀的骰子,向上的点数之差的绝对值为3的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
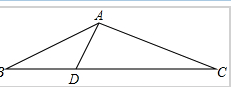 如图△ABC中,∠BAC=120°,AB=1,AC=2,D在BC上,且DC=4BD,则AD的长为
如图△ABC中,∠BAC=120°,AB=1,AC=2,D在BC上,且DC=4BD,则AD的长为