题目内容
已知曲线C的极坐标方程为ρ=
,直线l的参数方程为
(t为参数,0≤α<π).
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线l经过点(1,0),求直线l被曲线C截得的线段AB的长.
| 4cosθ |
| sin2θ |
|
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线l经过点(1,0),求直线l被曲线C截得的线段AB的长.
考点:直线的参数方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)利用
即可得出直角坐标方程;
(2)直线l的参数方程
( t为参数,0≤α<π).可得l经过点(0,1);若直线l经过点(1,0),得到α=
,得到直线l新的参数方程为
(t为参数).代入抛物线方程可得t2+2
t+2=0.设A、B对应的参数分别为t1,t2,利用|AB|=
即可得出.
|
(2)直线l的参数方程
|
| 3π |
| 4 |
|
| 6 |
| (t1+t2)2-4t1t2 |
解答:
解:(1)曲线C的极坐标方程ρ=
化为ρ2sin2θ=4ρcosθ,
得到曲线C的直角坐标方程为y2=4x,
故曲线C是顶点为O(0,0),焦点为F(1,0)的抛物线;
(2)直线l的参数方程为
( t为参数,0≤α<π).
故l经过点(0,1);
若直线l经过点(1,0),则α=
,
∴直线l的参数方程为
(t为参数).
代入y2=4x,得t2+2
t+2=0
设A、B对应的参数分别为t1,t2,则t1+t2=-2
,t1t2=2.
|AB|=|t1-t2|=
=
=4.
| 4cosθ |
| sin2θ |
得到曲线C的直角坐标方程为y2=4x,
故曲线C是顶点为O(0,0),焦点为F(1,0)的抛物线;
(2)直线l的参数方程为
|
故l经过点(0,1);
若直线l经过点(1,0),则α=
| 3π |
| 4 |
∴直线l的参数方程为
|
代入y2=4x,得t2+2
| 6 |
设A、B对应的参数分别为t1,t2,则t1+t2=-2
| 6 |
|AB|=|t1-t2|=
| (t1+t2)2-4t1t2 |
(-2
|
点评:本题考查了极坐标方程和直角坐标方程的转换、直线的参数方程及其应用,考查了计算能力,属于中档题..

练习册系列答案
相关题目
命题p:?x∈[0,+∞),(log32)x≤1,则下列说法正确的是( )
| A、p是假命题:¬p:?x0∈[0,+∞),(log32)x0>1 |
| B、p是假命题:¬p:?x∈[0,+∞),(log32)x≥1 |
| C、p是真命题:¬p:?x0∈[0,+∞),(log32)x0>1 |
| D、p是假命题:¬p:?x∈[0,+∞),(log32)x≥1 |
设集合M={x|y=
},集合N={y|y=x2,x∈M},则M∩N=( )
| x-2 |
| A、[2,+∞) |
| B、[4,+∞) |
| C、[0,+∞) |
| D、[0,4] |
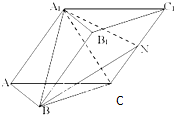 己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,N是CC1的中点.
己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,N是CC1的中点.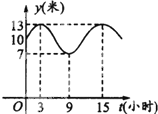 某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下表是水深数据:
某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下表是水深数据: