题目内容
已知x=a、x=b是函数f(x)=lnx+
x2-(m+2)x(m∈R)的两个极值点,若
≥4.
(Ⅰ)求实数m的取值范围;
(Ⅱ)求f(b)-f(a)的最大值.
| 1 |
| 2 |
| b |
| a |
(Ⅰ)求实数m的取值范围;
(Ⅱ)求f(b)-f(a)的最大值.
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:(1)先求出函数的定义域,接着求出函数的导数,由于x=a、x=b是函数f(x)=lnx+
x2-(m+2)x(m∈R)的两个极值点,所以x=a、x=b是f′(x)的2个根,根据导数的特点和
≥4可判断a,b是2个正值;
(2)把f(b)-f(a)的表达式求出来,利用导数求其最大值.
| 1 |
| 2 |
| b |
| a |
(2)把f(b)-f(a)的表达式求出来,利用导数求其最大值.
解答:
解:(Ⅰ)函数f(x)的定义域为(0,+∞),f′(x)=
+x-(m+2)=
.
由题意得:x=a、x=b是方程x2-(m+2)x+1=0的两个不等正根,且a<b,
∴
⇒m>0且a+b=m+2,ab=1. …3分
设t=
,则t≥4,(m+2)2=(a+b)2=
=t+
+2,
易知函数g(t)=t+
+2在[1,+∞)上单调递增,所以g(t)≥g(4)=
,所以m≥
.
故实数m的取值范围是[
,+∞). …6分
(Ⅱ)∵f(b)-f(a)=ln
+
(b2-a2)-(m+2)(b-a),
所以f(b)-f(a)=ln
+[
(b2-a2)-(a+b)(b-a)]•
=lnt-
(t-
).
构造函数h(t)=lnt-
(t-
)(其中t≥4),则h′(t)=
-
(1+
)=-
<0,
所以函数h(t)在[4,+∞)上单调递减,于是有h(t)≤h(4)=ln4-
.
故f(b)-f(a)的最大值为ln4-
. …13分.
| 1 |
| x |
| x2-(m+2)x+1 |
| x |
由题意得:x=a、x=b是方程x2-(m+2)x+1=0的两个不等正根,且a<b,
∴
|
设t=
| b |
| a |
| (a+b)2 |
| ab |
| 1 |
| t |
易知函数g(t)=t+
| 1 |
| t |
| 25 |
| 4 |
| 1 |
| 2 |
故实数m的取值范围是[
| 1 |
| 2 |
(Ⅱ)∵f(b)-f(a)=ln
| b |
| a |
| 1 |
| 2 |
所以f(b)-f(a)=ln
| b |
| a |
| 1 |
| 2 |
| 1 |
| ab |
| 1 |
| 2 |
| 1 |
| t |
构造函数h(t)=lnt-
| 1 |
| 2 |
| 1 |
| t |
| 1 |
| t |
| 1 |
| 2 |
| 1 |
| t2 |
| (t-1)2 |
| 2t2 |
所以函数h(t)在[4,+∞)上单调递减,于是有h(t)≤h(4)=ln4-
| 15 |
| 8 |
故f(b)-f(a)的最大值为ln4-
| 15 |
| 8 |
点评:本题主要考查导数的综合应用,利用导数判断函数的单调性、求其最值,属于中档题.

练习册系列答案
相关题目
设集合M={x∈Z|x2+2x≤0},N={x|x2-2x=0,x∈R},则M∩N=( )
| A、{0} |
| B、{0,2} |
| C、{-2,0} |
| D、{-2,0,2} |
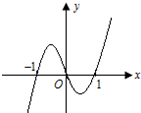 已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则以下说法错误的是( )
已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则以下说法错误的是( )| A、f′(1)+f′(-1)=0 |
| B、当x=-1时,函数f(x)取得极大值 |
| C、方程xf'(x)=0与f(x)=0均有三个实数根 |
| D、当x=1时,函数f(x)取得极小值 |
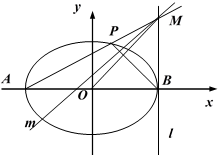 (1)求椭圆E的方程;
(1)求椭圆E的方程;