题目内容
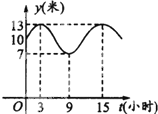 某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下表是水深数据:
某港口水深y(米)是时间t(0≤t≤24,单位:小时)的函数,下表是水深数据:| t(小时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
(1)试根据数据表和曲线,求出y=Asinωt+b的表达式;
(2)一般情况下,船舶航行时船底与海底的距离不小于4.5米是安全的,如果某船的吃水度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,它在港内停留的时间最多不能超过多长时间?(忽略离港所用的时间)
考点:在实际问题中建立三角函数模型
专题:应用题,三角函数的图像与性质
分析:(1)根据数据,
,可得A=3,h=10,由T=15-3=12,可求ω=
,将点(3,13)代入可得φ=0,从而可求函数的表达式;
(2)由题意,水深y≥4.5+7,即3sin
t+10≥11.5(0≤t≤24),从而可求t∈[1,5]或t∈[13,17];
|
| π |
| 6 |
(2)由题意,水深y≥4.5+7,即3sin
| π |
| 6 |
解答:
解:(1)根据数据,
,
∴A=3,h=10,
T=15-3=12,
∴ω=
=
,
∴y=3sin(
x+φ)+10
将点(3,13)代入可得π=0
∴函数的表达式为y=3sin
t+10(0≤t≤24);
(2)由题意,水深y≥4.5+7,
即3sin
t+10≥11.5(0≤t≤24),
∴sin
t≥
,
∴sin
t∈[2kπ+
,2kπ+
],k=0,1,
∴t∈[1,5]或t∈[13,17];
所以,该船在1:00至5:00或13:00至17:00能安全进港.
若欲于当天安全离港,它在港内停留的时间最多不能超过16小时.
|
∴A=3,h=10,
T=15-3=12,
∴ω=
| 2π |
| T |
| π |
| 6 |
∴y=3sin(
| π |
| 6 |
将点(3,13)代入可得π=0
∴函数的表达式为y=3sin
| π |
| 6 |
(2)由题意,水深y≥4.5+7,
即3sin
| π |
| 6 |
∴sin
| π |
| 6 |
| 1 |
| 2 |
∴sin
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴t∈[1,5]或t∈[13,17];
所以,该船在1:00至5:00或13:00至17:00能安全进港.
若欲于当天安全离港,它在港内停留的时间最多不能超过16小时.
点评:本题以表格数据为载体,考查三角函数模型的构建,考查解三角不等式,同时考查学生分析解决问题的能力.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 一个正方形被分成九个相等的小正方形,将中间的一个正方形挖去,如图(1);再将剩余的每个正方形都分成九个相等的小正方形,并将中间的一个挖去,得图(2);如此继续下去,则第n个图共挖去小正方形( )
一个正方形被分成九个相等的小正方形,将中间的一个正方形挖去,如图(1);再将剩余的每个正方形都分成九个相等的小正方形,并将中间的一个挖去,得图(2);如此继续下去,则第n个图共挖去小正方形( )| A、(8n-1)个 | ||
| B、(8n+1)个 | ||
C、
| ||
D、
|
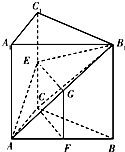 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,