题目内容

已知
a
=（
3
cosx-
3
，sinx），
b
=（1+cosx，cosx），设f（x）=
a
•
b
，求：
（1）f（x）的解析式并简化；
（2）求函数f（x）在区间[0，
π
6
]上的值域．
考点：平面向量的综合题
专题：平面向量及应用
分析：（1）由向量数量积运算化简即可得函数f（x）的解析式；
（2）由正弦函数图象及性质判断函数f（x）的单调性即可得出其最值，求出值域．
解答： 解：（1）f（x）=
a
•
b
=（
3
cosx-
3
）（1+cosx）+sinxcosx=
3
cos2x+sinxcosx-
3
=
3
2
（1+cos2x）+
1
2
sin2x-
3

=
3
2
c0s2x+
1
2
sin2x-
3
2
=sin（2x+
π
3
）-
3
2
．
∴f（x）=sin（2x+
π
3
）-
3
2
．
（2）∵x∈[0，
π
6
]，∴2x+
π
3
∈[
π
3
，
2π
3
]，
∴当2x+
π
3
=
π
3
或
2π
3
即x=0或
π
6
时，f（x）min=0，
当2x+
π
3
=
π
2
即x=
π
12
时，f（x）max=1-
3
2
=
2-
3
2
，
∴函数f（x）在区间[0，
π
6
]上的值域为[0，
2-
3
2
]．
点评：本题是向量与三角函数相结合的问题，考查学生数量积运算及三角函数的化简求最值问题，属于基础题．
练习册系列答案
相关题目
函数y=
log2(2x2-x)
的定义域为（　　）
A、{x|x≤-
1
2
，或x≥1}
B、{x|x＜-
1
2
，或x＞1}
C、{x|x≤0，或x≥
1
2
}
D、{x|x＜0，或x＞
1
2
}
观察圆周上n个点之间所边的弦，发现两个点可以连一条弦，3个点可以连3条弦，4个点可以连6条弦，5个点可以连10条弦，以此类推可以归纳出n个点之间所连弦的条数为
 
．
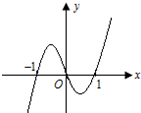已知函数y=xf′（x）的图象如图所示（其中f′（x）是函数f（x）的导函数），则以下说法错误的是（　　）
A、f′（1）+f′（-1）=0
B、当x=-1时，函数f（x）取得极大值
C、方程xf'（x）=0与f（x）=0均有三个实数根
D、当x=1时，函数f（x）取得极小值
已知曲线C的极坐标方程为ρ=
4cosθ
sin2θ
，直线l的参数方程为
x=tcosα
y=1+tsinα
（t为参数，0≤α＜π）．
（Ⅰ）把曲线C的极坐标方程化为直角坐标方程，并说明曲线C的形状；
（Ⅱ）若直线l经过点（1，0），求直线l被曲线C截得的线段AB的长．
已知函数f（x）=
x
x+1
，数列{an}满足a1=1，an+1=f（an）．
（1）求证：数列{
1
an
}是等差数列；
（2）设bn=anan+1，记数列{bn}的前n项和为sn，求证：
1
2
≤sn＜1．
如图，在平面直角坐标系xOy中，椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦距为2，且过点（
2
，
6
2
）．
（1）求椭圆E的方程；
（2）若点A，B分别是椭圆E的左、右顶点，直线l经过点B且垂直于x轴，点P是椭圆上异于A，B的任意一点，直线AP交l于点M．
①设直线OM的斜率为k1，直线BP的斜率为k2，求证：k1k2为定值；
②设过点M垂直于PB的直线为m．求证：直线m过定点，并求出定点的坐标．
已知向量
a
=（cosx，sinx），
b
=（-cosx，xosx），
c
=（-1，0）
（1）若x=
π
6
，求
a
，
c
的夹角；
（2）求函数f（x）=2
a
•
b
+1的单调递增区间．
一个正方形被分成九个相等的小正方形，将中间的一个正方形挖去，如图（1）；再将剩余的每个正方形都分成九个相等的小正方形，并将中间的一个挖去，得图（2）；如此继续下去，则第n个图共挖去小正方形（　　）
A、（8n-1）个
B、（8n+1）个
C、
1
7
（8n-1）个
D、
1
7
（8n+1）个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网