题目内容
已知直线l的方程为kx-y+1=0(k∈R),圆C的方程为x2+y2-2x-3=0.
(1)试判断直线与圆C的位置关系,并说明理由.
(2)过点(0,1)作直线l1⊥l,设直线l1与圆C相交于M,N两点,直线l与圆C相交于P,Q两点,则四边形PMQN的面积是否存在最大值和最小值?若存在,请求出,否则说明理由.
(1)试判断直线与圆C的位置关系,并说明理由.
(2)过点(0,1)作直线l1⊥l,设直线l1与圆C相交于M,N两点,直线l与圆C相交于P,Q两点,则四边形PMQN的面积是否存在最大值和最小值?若存在,请求出,否则说明理由.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)首先求出直线恒过的定点(0,1)进一步判断点与圆的位置关系,从而确定直线与圆的位置关系
(2)根据直线与直线垂直,并且还判断出直线都过(0,1)点,并进一步求出结果.
(2)根据直线与直线垂直,并且还判断出直线都过(0,1)点,并进一步求出结果.
解答:
解:(1)结论:直线与圆C的位置关系是:相交
理由:已知直线l的方程为kx-y+1=0(k∈R)
则直线l恒过(0,1)点,圆C的方程为x2+y2-2x-3=0转化为:(x-1)2+y2=4 R=2
点(0,1)到圆心的距离为
<2=R
所以点(0,1)在圆内,即直线与圆相交
(2)由(1)得直线l恒过(0,1)点,过点(0,1)作直线l1⊥l,则直线l1的直线方程为:y=-
x+1
则这条直线也恒过(0,1),圆C的方程为x2+y2-2x-3=0转化为:(x-1)2+y2=4
所以:直线l1与圆C相交于M,N两点,直线l与圆C相交于P,Q两点构成的四边形,当直线MN的斜率不存在时,由于MN⊥PQ,则四边形PMQN的面积为最大值.
S max=
•2
•2
=18.
当k=±1时,利用圆心到直线的距离d=
所以:两条对角线的长都为4,由于对角线互相垂直,
所以:Smin=
•4•4=8.
理由:已知直线l的方程为kx-y+1=0(k∈R)
则直线l恒过(0,1)点,圆C的方程为x2+y2-2x-3=0转化为:(x-1)2+y2=4 R=2
点(0,1)到圆心的距离为
| 2 |
所以点(0,1)在圆内,即直线与圆相交
(2)由(1)得直线l恒过(0,1)点,过点(0,1)作直线l1⊥l,则直线l1的直线方程为:y=-
| 1 |
| k |
则这条直线也恒过(0,1),圆C的方程为x2+y2-2x-3=0转化为:(x-1)2+y2=4
所以:直线l1与圆C相交于M,N两点,直线l与圆C相交于P,Q两点构成的四边形,当直线MN的斜率不存在时,由于MN⊥PQ,则四边形PMQN的面积为最大值.
S max=
| 1 |
| 2 |
| 3 |
| 3 |
当k=±1时,利用圆心到直线的距离d=
| 2 |
所以:两条对角线的长都为4,由于对角线互相垂直,
所以:Smin=
| 1 |
| 2 |
点评:本题考查的知识点:点、直线与圆的位置关系,恒过定点的直线,直线和圆相交的特殊情况,属于中档题.

练习册系列答案
相关题目
设集合M={x∈Z|x2+2x≤0},N={x|x2-2x=0,x∈R},则M∩N=( )
| A、{0} |
| B、{0,2} |
| C、{-2,0} |
| D、{-2,0,2} |
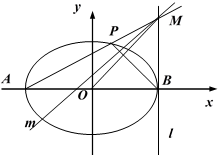 (1)求椭圆E的方程;
(1)求椭圆E的方程;