题目内容
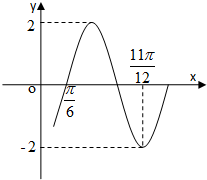 函数y=Asin(ωx+φ)的部分图象如图所示,其中A>0,ω>0,|φ|<
函数y=Asin(ωx+φ)的部分图象如图所示,其中A>0,ω>0,|φ|<| π |
| 2 |
A、y=2sin(2x-
| ||||
B、y=2sin(x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:根据函数的图象,得出
T的值,求出ω的值;得出A的值,再由x=
时,y=0,求出φ的值即可.
| 3 |
| 4 |
| π |
| 6 |
解答:
解:根据函数的图象,得;
T=
-
=
π,
∴T=π,
∴ω=
=2;
又A=2,
x=
时,y=0,
∴2×
+φ=0,
∴φ=-
;
∴f(x)=2sin(2x-
).
故选:A.
| 3 |
| 4 |
| 11π |
| 12 |
| π |
| 6 |
| 3 |
| 4 |
∴T=π,
∴ω=
| 2π |
| T |
又A=2,
x=
| π |
| 6 |
∴2×
| π |
| 6 |
∴φ=-
| π |
| 3 |
∴f(x)=2sin(2x-
| π |
| 3 |
故选:A.
点评:本题考查了三角函数的图象与性质的应用问题,解题时应根据图象求出对应的ω、A和φ的值,是基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知f(x)=
,则f(-2)=( )
|
| A、-1 | B、3 | C、5 | D、1 |
已知函数f(x)=
,则满足f(x)=
的x的值为( )
|
| 1 |
| 2 |
A、
| ||||
| B、-1 | ||||
C、
| ||||
D、
|
已知点(3,1)和(-1,5)在直线3x-2y+a=0的两侧,则a的取值范围是( )
| A、a<-7或 a>13 |
| B、-7<a<13 |
| C、a=7 或 a=13 |
| D、-13<a<7 |
已知F1,F2分别是椭圆C1和双曲线C2的公共的左右焦点,e1、e2是C1、C2的离心率,若C1、C2在第一象限内的交点为P,且满足∠POF2=2∠PF1F2,则e1、e2的关系是( )
| A、e12+e22=2e12e22 |
| B、e12+e1e2+e22=2 |
| C、e12+e22=2 |
| D、e1e2=2 |
已知“x>2”是“x2>a(a∈R)”的充分不必要条件,则a的取值范围是( )
| A、(-∞,4) |
| B、(4,+∞) |
| C、(0,4] |
| D、(-∞,4] |
 如图,F1、F2是双曲线
如图,F1、F2是双曲线 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这点开始跳,则经过2012次跳后,它停在的点所对应的数为( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这点开始跳,则经过2012次跳后,它停在的点所对应的数为( )