题目内容

已知f（x）=
x+1x＞1
-x+3x≤1
，则f（-2）=（　　）
A、-1B、3C、5D、1
考点：函数的值
专题：函数的性质及应用
分析：利用分段函数的性质求解．
解答： 解：∵f（x）=
x+1x＞1
-x+3x≤1
，
∴f（-2）=-（-2）+3=5．
故选：C．
点评：本题考查函数值的求法，解题时要认真审题，注意分段函数的性质的合理运用．
练习册系列答案
相关题目
已知幂函数f（x）=k•xα（k，α∈R）的图象过点（
1
2
，
2
2
），则k+α=
 
．
空间中任意放置的棱长为2的正四面体ABCD，下列命题正确的是
 
．（写出所有正确命题的编号）
①正四面体ABCD的主视图面积可能是
2
；
②正四面体ABCD的主视图面积可能是
2
6
3
；
③正四面体ABCD的主视图面积可能是
3
；
④正四面体ABCD的主视图面积可能是2；
⑤正四面体ABCD的主视图面积可能是4．
已知f（x）=-asinx-bx3+2，且f（2011）=-6，则f（-2011）的值为
 
．
函数y=x3是（　　）
A、偶函数且是增函数
B、奇函数且是增函数
C、偶函数且是减函数
D、奇函数且是减函数
函数f（x）=x2-2ax+2在（-∞，3）上递减，则a的取值范围是（　　）
A、[-3，+∞）
B、（-∞，-3]
C、（-∞，3}
D、[3，+∞）
已知函数sgn（x）=
1 ，x＞0
0，x=0
-1 ，x＜0
，f（x）=x2•sgn[1+sgn（x）]+2x•sgn[1-sgn（x）]，若函数g（x）=f（x）-m有两个零点，则m的取值范围是（　　）
A、m＜0B、0＜m＜1
C、0＜m≤1D、m＞1
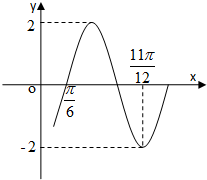函数y=Asin（ωx+φ）的部分图象如图所示，其中A＞0，ω＞0，|φ|＜
π
2
，则其解析式为（　　）
A、y=2sin（2x-
π
3
）
B、y=2sin（x+
π
3
）
C、y=2sin（
1
2
x-
π
6
）
D、y=2sin（2x+
π
6
）
在同一个坐标系中，函数y=3x与y=log 
1
3
x的图象最可能是（　　）
A、
B、
C、
D、

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网