题目内容
已知F1,F2分别是椭圆C1和双曲线C2的公共的左右焦点,e1、e2是C1、C2的离心率,若C1、C2在第一象限内的交点为P,且满足∠POF2=2∠PF1F2,则e1、e2的关系是( )
| A、e12+e22=2e12e22 |
| B、e12+e1e2+e22=2 |
| C、e12+e22=2 |
| D、e1e2=2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先确定PF1⊥PF2,再利用勾股定理、椭圆、双曲线的定义,即可得出结论.
解答:
解:∵∠POF2=2∠PF1F2,
∴∠OPF1=∠PF1F2,
∴OP=c,
∴PF1⊥PF2,
设|PF1|=m,|PF2|=n,则m2+n2=4c2,
∵m+n=2a,m-n=2a′,
∴m=a+a′,n=a-a′,
∴a2+a′2=2c2,
∴e12+e22=2e12e22,
故选:A.
∴∠OPF1=∠PF1F2,
∴OP=c,
∴PF1⊥PF2,
设|PF1|=m,|PF2|=n,则m2+n2=4c2,
∵m+n=2a,m-n=2a′,
∴m=a+a′,n=a-a′,
∴a2+a′2=2c2,
∴e12+e22=2e12e22,
故选:A.
点评:本题考查椭圆、双曲线的定义与性质,考查学生的计算能力,确定PF1⊥PF2是关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
函数f(x)=x2-2ax+2在(-∞,3)上递减,则a的取值范围是( )
| A、[-3,+∞) |
| B、(-∞,-3] |
| C、(-∞,3} |
| D、[3,+∞) |
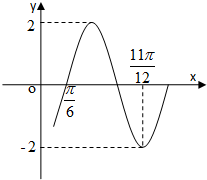 函数y=Asin(ωx+φ)的部分图象如图所示,其中A>0,ω>0,|φ|<
函数y=Asin(ωx+φ)的部分图象如图所示,其中A>0,ω>0,|φ|<| π |
| 2 |
A、y=2sin(2x-
| ||||
B、y=2sin(x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
sin390°的值是( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
下列说法中:①经过圆柱任意两条母线的截面是一个矩形;②连结圆柱上、下底面圆周上两点的线段是圆柱的母线;③圆柱的任意两条母线互相平行;④圆柱的侧面展开图是矩形;⑤圆柱的母线有且只有一条.其中正确命题的个数为( )
| A、3 | B、1 | C、2 | D、0 |
复数z=
(i为虚数单位),则z的共轭复数z为( )
| 3+i |
| 1+i |
| A、2-i | B、2+i |
| C、4-2i | D、4+2i |
函数y=x
的图象是( )
| 1 |
| 3 |
A、 |
B、 |
C、 |
D、 |