题目内容

已知点（3，1）和（-1，5）在直线3x-2y+a=0的两侧，则a的取值范围是（　　）
A、a＜-7或 a＞13
B、-7＜a＜13
C、a=7 或 a=13
D、-13＜a＜7
考点：二元一次不等式（组）与平面区域,直线的斜率
专题：不等式的解法及应用
分析：由题意可得（3×3-2×1+a）（-3×1-2×5+a）＜0，解不等式可得．
解答： 解：∵点（3，1）和（-1，5）在直线3x-2y+a=0的两侧，
∴（3×3-2×1+a）（-3×1-2×5+a）＜0，即（a+7）（a-13）＜0
解得-7＜a＜13
故选：B
点评：本题考查不等式与平面区域，属基础题．
练习册系列答案
相关题目
已知椭圆的方程为
x2
25
+
y2
16
=1，过右焦点F的直线交椭圆于A、B两点，则
|FA|
|FB|
取值范围为
 
．
函数y=x3是（　　）
A、偶函数且是增函数
B、奇函数且是增函数
C、偶函数且是减函数
D、奇函数且是减函数
已知函数sgn（x）=
1 ，x＞0
0，x=0
-1 ，x＜0
，f（x）=x2•sgn[1+sgn（x）]+2x•sgn[1-sgn（x）]，若函数g（x）=f（x）-m有两个零点，则m的取值范围是（　　）
A、m＜0B、0＜m＜1
C、0＜m≤1D、m＞1
已知函数f（x）=
x3，x≥1
2x-x2，x＜1
，若不等式f（m+1）≥f（tm-1）对任意m∈[-1，1]恒成立，则实数t的取值范围是（　　）
A、[-1，1]∪（1，3]
B、[-1，3]
C、[1，3]
D、（-∞，-1]∪[3，+∞）
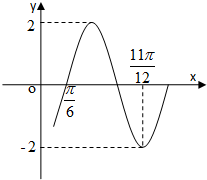函数y=Asin（ωx+φ）的部分图象如图所示，其中A＞0，ω＞0，|φ|＜
π
2
，则其解析式为（　　）
A、y=2sin（2x-
π
3
）
B、y=2sin（x+
π
3
）
C、y=2sin（
1
2
x-
π
6
）
D、y=2sin（2x+
π
6
）
（文科）直线l的方程为
3
x+y-2
3
=0，则直线l的倾斜角为（　　）
A、
5π
6
B、
2π
3
C、
π
3
D、
π
6
计算：
∫
2
0
|1-x2|dx=（　　）
A、-
2
3
B、
2
3
C、2
D、
8
3
如图所示的算法框图中，输出S的值为（　　）
A、10B、12C、15D、18

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网