题目内容
函数y=sinx+
的值域为 .
| 2 |
| sinx |
考点:正弦函数的定义域和值域
专题:函数的性质及应用,三角函数的图像与性质
分析:用换元法,设t=sinx,t∈[-1,1];把函数y=sinx+
化为y=t+
(t≠0),利用函数的单调性求出y的值域.
| 2 |
| sinx |
| 2 |
| t |
解答:
解:设t=sinx,t∈[-1,1];
∴函数y=sinx+
可化为
y=t+
,(t≠0);
∴y′=1-
,
当t∈[-1,0)时,y′<0,函数y是减函数,∴y≤-3;
当t∈(0,1]时,y′<0,函数y是减函数,∴y≥3;
∴函数y的值域为(-∞,-3]∪[3,+∞).
故答案为:(-∞,-3]∪[3,+∞).
∴函数y=sinx+
| 2 |
| sinx |
y=t+
| 2 |
| t |
∴y′=1-
| 2 |
| t2 |
当t∈[-1,0)时,y′<0,函数y是减函数,∴y≤-3;
当t∈(0,1]时,y′<0,函数y是减函数,∴y≥3;
∴函数y的值域为(-∞,-3]∪[3,+∞).
故答案为:(-∞,-3]∪[3,+∞).
点评:本题考查了利用函数的单调性求函数的值域的问题,解题时应考虑函数sinx的有界性,是基础题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
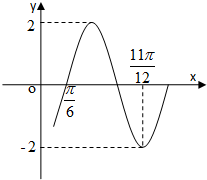 函数y=Asin(ωx+φ)的部分图象如图所示,其中A>0,ω>0,|φ|<
函数y=Asin(ωx+φ)的部分图象如图所示,其中A>0,ω>0,|φ|<| π |
| 2 |
A、y=2sin(2x-
| ||||
B、y=2sin(x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|