题目内容
 如图,F1、F2是双曲线
如图,F1、F2是双曲线| x2 |
| a2 |
| y2 |
| 24 |
| A、8 | ||
B、8
| ||
C、8
| ||
| D、16 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据双曲线的定义算出△AF1F2中,|AF1|=2a,|AF2|=4a,由△ABF2是等边三角形得∠F1AF2=120°,利用余弦定理算出c=
a,可得a=2,即可求出△BF1F2的面积
| 7 |
解答:
解: 根据双曲线的定义,可得|BF1|-|BF2|=2a,
根据双曲线的定义,可得|BF1|-|BF2|=2a,
∵△ABF2是等边三角形,即|BF2|=|AB|
∴|BF1|-|BF2|=2a,即|BF1|-|AB|=|AF1|=2a
又∵|AF2|-|AF1|=2a,
∴|AF2|=|AF1|+2a=4a,
∵△AF1F2中,|AF1|=2a,|AF2|=4a,∠F1AF2=120°
∴|F1F2|2=|AF1|2+|AF2|2-2|AF1|•|AF2|cos120°
即4c2=4a2+16a2-2×2a×4a×(-
)=28a2,解之得c=
a,
∴a2+24=7a2,∴a=2,
∴△BF1F2的面积为S△BF1F2-S△ABF2=
×8×12×
-
×(4×2)2=8
.
故选:C.
 根据双曲线的定义,可得|BF1|-|BF2|=2a,
根据双曲线的定义,可得|BF1|-|BF2|=2a,∵△ABF2是等边三角形,即|BF2|=|AB|
∴|BF1|-|BF2|=2a,即|BF1|-|AB|=|AF1|=2a
又∵|AF2|-|AF1|=2a,
∴|AF2|=|AF1|+2a=4a,
∵△AF1F2中,|AF1|=2a,|AF2|=4a,∠F1AF2=120°
∴|F1F2|2=|AF1|2+|AF2|2-2|AF1|•|AF2|cos120°
即4c2=4a2+16a2-2×2a×4a×(-
| 1 |
| 2 |
| 7 |
∴a2+24=7a2,∴a=2,
∴△BF1F2的面积为S△BF1F2-S△ABF2=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 3 |
故选:C.
点评:本题给出经过双曲线左焦点的直线被双曲线截得弦AB与右焦点构成等边三角形,求双曲线的离心率,着重考查了双曲线的定义和简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
已知函数sgn(x)=
,f(x)=x2•sgn[1+sgn(x)]+2x•sgn[1-sgn(x)],若函数g(x)=f(x)-m有两个零点,则m的取值范围是( )
|
| A、m<0 | B、0<m<1 |
| C、0<m≤1 | D、m>1 |
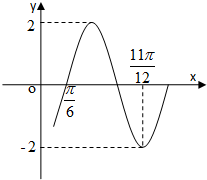 函数y=Asin(ωx+φ)的部分图象如图所示,其中A>0,ω>0,|φ|<
函数y=Asin(ωx+φ)的部分图象如图所示,其中A>0,ω>0,|φ|<| π |
| 2 |
A、y=2sin(2x-
| ||||
B、y=2sin(x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
(文科)直线l的方程为
x+y-2
=0,则直线l的倾斜角为( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法中:①经过圆柱任意两条母线的截面是一个矩形;②连结圆柱上、下底面圆周上两点的线段是圆柱的母线;③圆柱的任意两条母线互相平行;④圆柱的侧面展开图是矩形;⑤圆柱的母线有且只有一条.其中正确命题的个数为( )
| A、3 | B、1 | C、2 | D、0 |
计算:
|1-x2|dx=( )
| ∫ | 2 0 |
A、-
| ||
B、
| ||
| C、2 | ||
D、
|
在同一个坐标系中,函数y=3x与y=log
x的图象最可能是( )
| 1 |
| 3 |
A、 |
B、 |
C、 |
D、 |
(x
+
)11的展开式中,常数项是( )
| x |
| 1 |
| x4 |
| A、第3项 | B、第4项 |
| C、第7项 | D、第8项 |