题目内容
 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这点开始跳,则经过2012次跳后,它停在的点所对应的数为( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这点开始跳,则经过2012次跳后,它停在的点所对应的数为( )| A、1 | B、2 | C、3 | D、5 |
考点:归纳推理
专题:计算题,推理和证明
分析:根据题意,分析可得青蛙的跳动规律为2-1-3-5,周期为4;又由2012=4×502+4,经过2012次跳后它停在的点所对应的数为5.
解答:
解:由5起跳,5是奇数,沿顺时针下一次能跳2个点,落在2上.
由2起跳,2是偶数,沿逆时针下一次只能跳一个点,落在1上
1是奇数,沿顺时针跳两个点,落在3上.
由3起跳,是奇偶数,沿顺时针跳两个点,落在5上.
2-1-3-5-2,周期为4;又由2012=4×502+4,
∴经过2012次跳后它停在的点所对应的数为5.
故选:D.
由2起跳,2是偶数,沿逆时针下一次只能跳一个点,落在1上
1是奇数,沿顺时针跳两个点,落在3上.
由3起跳,是奇偶数,沿顺时针跳两个点,落在5上.
2-1-3-5-2,周期为4;又由2012=4×502+4,
∴经过2012次跳后它停在的点所对应的数为5.
故选:D.
点评:此题主要考查了数的变化规律,得到青蛙落在数字上的循环规律是解决本题的关键.

练习册系列答案
相关题目
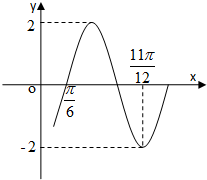 函数y=Asin(ωx+φ)的部分图象如图所示,其中A>0,ω>0,|φ|<
函数y=Asin(ωx+φ)的部分图象如图所示,其中A>0,ω>0,|φ|<| π |
| 2 |
A、y=2sin(2x-
| ||||
B、y=2sin(x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
在同一个坐标系中,函数y=3x与y=log
x的图象最可能是( )
| 1 |
| 3 |
A、 |
B、 |
C、 |
D、 |
复数
满足(1-i)
=1+i,其中i为虚数单位,则
=( )
. |
| z |
. |
| z |
. |
| z |
| A、-1 | B、1 | C、-i | D、i |
如图所示的算法框图中,输出S的值为( )


| A、10 | B、12 | C、15 | D、18 |
函数y=x
的图象是( )
| 1 |
| 3 |
A、 |
B、 |
C、 |
D、 |
(x
+
)11的展开式中,常数项是( )
| x |
| 1 |
| x4 |
| A、第3项 | B、第4项 |
| C、第7项 | D、第8项 |