题目内容
已知函数f(x)对任意x∈R,都有f(x)=1-f(1-x),则f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)= .
考点:函数的值,抽象函数及其应用
专题:函数的性质及应用
分析:灵活利用赋值法即可求出值
解答:
解:f(x)=1-f(1-x),
令x=0,则f(0)=1-f(1),即f(0)+f(1)=1
令x=2,则f(2)=1-f(-1),即f(-1)+f(2)=1
令x=3,则f(3)=1-f(-2),即f(-2)+f(3)=1
∴f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)=1+1+1=3
故答案为:3
令x=0,则f(0)=1-f(1),即f(0)+f(1)=1
令x=2,则f(2)=1-f(-1),即f(-1)+f(2)=1
令x=3,则f(3)=1-f(-2),即f(-2)+f(3)=1
∴f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)=1+1+1=3
故答案为:3
点评:本题考查了抽象函数的问题,灵活利用赋值是关键,属于基础题

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
函数f(x)=x
-
的零点所在的区间是( )
| 1 |
| 3 |
| 1 |
| 2x |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
已知函数y=f(x)-1为奇函数,且f(x)的最大值为M,最小值为N,则有( )
| A、M-N=4 |
| B、M-N=2 |
| C、M+N=2 |
| D、M+N=4 |
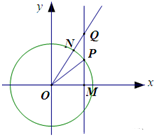
 京广高铁的贯通,带动了沿线某站点所在市旅游业的发展.在车站附近,有一块边长为100m的正方形地皮,如图ABCD所示,其中AST是一半径为90m的扇形小山,其余部分都是平地.市政府决定在平地上建一个矩形停车场,使矩形的一个顶点P在弧ST上,相邻两边CQ、CR落在正方形的边BC、CD上.求矩形停车场PQCR面积S的最大值与最小值.
京广高铁的贯通,带动了沿线某站点所在市旅游业的发展.在车站附近,有一块边长为100m的正方形地皮,如图ABCD所示,其中AST是一半径为90m的扇形小山,其余部分都是平地.市政府决定在平地上建一个矩形停车场,使矩形的一个顶点P在弧ST上,相邻两边CQ、CR落在正方形的边BC、CD上.求矩形停车场PQCR面积S的最大值与最小值.