题目内容
若点(a,27)在函数y=3x的图象上,则tan
的值为 .
| π |
| a |
考点:指数函数的定义、解析式、定义域和值域
专题:函数的性质及应用
分析:根据点与曲线的关系求出a的值,然后代入即可得到三角值.
解答:
解:∵点(a,27)在函数y=3x的图象上,
∴3a=27=33,即a=3.
则tan
=tan
=
,
故答案为:
∴3a=27=33,即a=3.
则tan
| π |
| a |
| π |
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题主要考查函数值的计算,利用点与曲线的关系求出a的值是解决本题的关键,比较基础.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
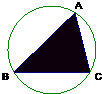 如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )
如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数y=f(x),数列{an}的通项公式是an=f(n),n∈N*,那么“函数y=f(x)在[1,+∞﹚上单调递增”是“数列{an}是递增数列”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
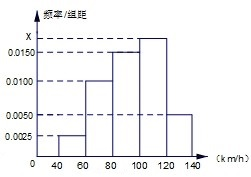 根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有
根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有