题目内容
若点P(x,y)在曲线
(θ为参数,θ∈R)上,则
的取值范围是 .
|
| y |
| x |
考点:圆的参数方程
专题:直线与圆
分析:将曲线C的参数方程
(θ为参数,θ∈R)化为直角坐标方程,令
=k,作出两曲线的图象,利用点到直线间的距离公式即可求得答案.
|
| y |
| x |
解答:
解:∵曲线C的参数方程为
(θ为参数),
∴其直角坐标方程为:x2+(y-2)2=1;
又
=
,其几何意义为:曲线C上的点P与坐标原点O的斜率,
令
=k,则y=kx,
作图如下:
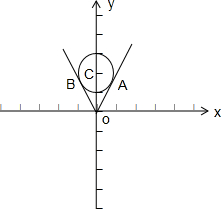
设点C到直线y=kx的距离为d,则d=
=
,
∵点P(x,y)为x2+(y-2)2=1上的点,
∴
≤1,
∴k2+1≥4,
解得k≥
或k≤-
,
∴
的取值范围是(-∞,-
]∪[
,+∞).
故答案为:(-∞,-
]∪[
,+∞).
|
∴其直角坐标方程为:x2+(y-2)2=1;
又
| y |
| x |
| y-0 |
| x-0 |
令
| y |
| x |
作图如下:

设点C到直线y=kx的距离为d,则d=
| |k×0-2| | ||
|
| 2 | ||
|
∵点P(x,y)为x2+(y-2)2=1上的点,
∴
| 2 | ||
|
∴k2+1≥4,
解得k≥
| 3 |
| 3 |
∴
| y |
| x |
| 3 |
| 3 |
故答案为:(-∞,-
| 3 |
| 3 |
点评:本题考查圆的参数方程,考查点到直线间的距离公式的应用,考查数形结合思想与运算求解能力,属于中档题.

练习册系列答案
相关题目
已知
=(1,2),
=(3,4),则向量
在
方向上的投影为( )
| a |
| b |
| b |
| a |
| A、5 | ||||
B、
| ||||
| C、3 | ||||
D、
|
“m>n>1”是“logm2<logn2”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
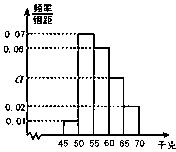 为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.则a=
为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.则a=