题目内容
函数f（x）=ax2+2（a-2）x+3在区间（-∞，3]上为减函数，则a的取值范围为 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：先对函数f（x）进行求导，由题意得f′（x）=2ax+2a-4≤0在区间（-∞，3]恒成立，列出不等式组，求出a的范围即可．
解答：
解：∵f（x）=ax2+2（a-2）x+3，
∴f′（x）=2ax+2a-4，
∵函数f（x）=ax2+2（a-2）x+3在区间（-∞，3]上为减函数，
∴2ax+2a-4≤0在区间（-∞，3]恒成立．
∴
，
解得：0≤a≤
，
故a的取值范围为：[0，
]，
故答案为：[0，
]．
∴f′（x）=2ax+2a-4，
∵函数f（x）=ax2+2（a-2）x+3在区间（-∞，3]上为减函数，
∴2ax+2a-4≤0在区间（-∞，3]恒成立．
∴
|
解得：0≤a≤
| 1 |
| 2 |
故a的取值范围为：[0，
| 1 |
| 2 |
故答案为：[0，
| 1 |
| 2 |
点评：本题考查的知识点是二次函数的性质，其中熟练掌握导数法确定函数单调性的方法是解答的关键．
练习册系列答案
相关题目
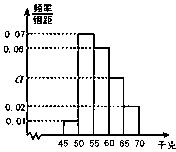为了解学生的身体状况，某校随机抽取了一批学生测量体重．经统计，这批学生的体重数据（单位：千克）全部介于45至70之间．将数据分成以下5组：第1组[45，50），第2组[50，55），第3组[55，60），第4组[60，65），第5组[65，70]，得到如图所示的频率分布直方图．则a=己知集合A={x|x2-3x+2＜0}，B={x|log4x＞
}，则（ ）
| 1 |
| 2 |
| A、A∩B=∅ |
| B、B⊆A |
| C、A∩∁RB=R |
| D、A⊆B |
已知
=（1，2），
=（3，4），则向量
在
方向上的投影为（ ）
| a |
| b |
| b |
| a |
| A、5 | ||||
B、
| ||||
| C、3 | ||||
D、
|
已知i是虚数单位，复数z=
，则z的共轭复数
等于（ ）
| 4+3i |
| 1+2i |
. |
| z |
| A、-2+i | B、-2-i |
| C、2+i | D、2-i |