题目内容
设数列{an}中,a1=2,an+1=an+n+1,则通项an= .
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:利用累加法即可求得答案.
解答:
解:∵an+1=an+n+1,
∴n≥2时,a2-a1=2,a3-a2=3,…,an-an-1=n,
以上各式相加,得an-a1=
,
an=
(n2+n+2),
又a1=2适合上式,∴an=
(n2+n+2),
故答案为:an=
(n2+n+2).
∴n≥2时,a2-a1=2,a3-a2=3,…,an-an-1=n,
以上各式相加,得an-a1=
| (n-1)(n+2) |
| 2 |
an=
| 1 |
| 2 |
又a1=2适合上式,∴an=
| 1 |
| 2 |
故答案为:an=
| 1 |
| 2 |
点评:该题考查由数列递推式求数列通项,属基础题,累加法是求数列通项的基本方法,要熟练掌握.

练习册系列答案
相关题目
已知a、b∈R,“a<b”是“2a<3b”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
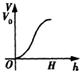
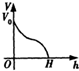
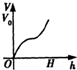
 一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
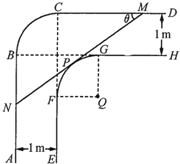 一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m.