题目内容
 一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )A、 |
B、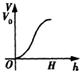 |
C、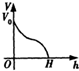 |
D、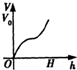 |
考点:函数的图象
专题:数形结合
分析:水深h越大,水的体积v就越大,故函数v=f(h)是个增函数,一开始增长越来越快,后来增长越来越慢,图象是先凹后凸的.
解答:
解:由图得水深h越大,水的体积v就越大,故函数v=f(h)是个增函数. 据四个选项提供的信息,
当h∈[O,H],我们可将水“流出”设想成“流入”,
这样每当h增加一个单位增量△h时,
根据鱼缸形状可知,函数V的变化,开始其增量越来越大,但经过中截面后则增量越来越小,
故V关于h的函数图象是先凹后凸的,曲线上的点的切线斜率先是逐渐变大,后又逐渐变小,
故选D.
当h∈[O,H],我们可将水“流出”设想成“流入”,
这样每当h增加一个单位增量△h时,
根据鱼缸形状可知,函数V的变化,开始其增量越来越大,但经过中截面后则增量越来越小,
故V关于h的函数图象是先凹后凸的,曲线上的点的切线斜率先是逐渐变大,后又逐渐变小,
故选D.
点评:本题考查了函数图象的变化特征,函数的单调性的实际应用,体现了数形结合的数学思想和逆向思维.

练习册系列答案
相关题目
函数y=(cosx+sinx)•(cosx-sinx)的最小正周期是( )
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
函数f(x)=
的图象大致是( )
| x3-3 |
| ex |
A、 |
B、 |
C、 |
D、 |
已知△ABC的内角A、B、C的对边分别为a、b、c,若a2-c2=b2+bc,则A=( )
| A、30° | B、60° |
| C、120° | D、150° |
在△ABC中,6sinA+4cosB=1,且4sinB+6cosA=5
,则cosC=( )
| 3 |
A、
| ||||
B、±
| ||||
C、
| ||||
D、-
|
若沿△ABC三条边的中位线折起能拼成一个三棱锥,则△ABC( )
| A、一定是等边三角形 |
| B、一定是锐角三角形 |
| C、可以是直角三角形 |
| D、可以是钝角三角形 |



