题目内容
已知sinθ-cosθ=
cos5°-
sin5°,θ∈(0,2π),求角θ的值.
| ||
| 2 |
| ||
| 2 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:由两角和与差的正弦函数公式化简等式可得
sin(θ-45°)=
sin25°=
sin155°,由θ∈(0,2π),即可解得角θ的值.
| 2 |
| 2 |
| 2 |
解答:
解:sinθ-cosθ=
cos5°-
sin5°,θ∈(0,2π),
⇒
sin(θ-45°)=
cos65°=
sin25°=
sin155°
⇒θ-45°=25°或θ-45°=155°
⇒θ=70°或200°
| ||
| 2 |
| ||
| 2 |
⇒
| 2 |
| 2 |
| 2 |
| 2 |
⇒θ-45°=25°或θ-45°=155°
⇒θ=70°或200°
点评:本题主要考查了两角和与差的正弦函数公式的应用,考查了诱导公式的应用,熟练使用相关公式是解题的关键,使用基本知识的考查.

练习册系列答案
相关题目
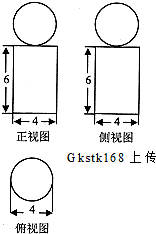 如图是一个空间几何体的三视图(注:正视图也称主视图,侧视图也称左视图),其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成,俯视图是直径等于4的圆,该几何体的体积是( )
如图是一个空间几何体的三视图(注:正视图也称主视图,侧视图也称左视图),其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成,俯视图是直径等于4的圆,该几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
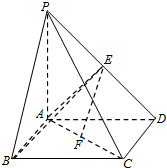 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AB=2,E,F分别为PD,AC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AB=2,E,F分别为PD,AC的中点.