题目内容
| 3 | a |
| 3 | b |
| 3 | a-b |
| A、ab（b-a）＞0 |
| B、ab＞0且a＞b |
| C、ab＜0且a＜b |
| D、ab（b-a）＜0 |
考点：必要条件、充分条件与充要条件的判断
专题：不等式的解法及应用,简易逻辑
分析：根据两数差的立方公式，将不等式进行化简，结合不等式的性质即可得到结论．
解答：
解：
-
＜
成立的等价条件是：
a-3（
）2（
）+3（
）（
）2-b＜a-b，
即3（
）（
）（
-
）＜0，
即ab（
-
）＜0，
即ab（b-a）＜0，
故选：D
| 3 | a |
| 3 | b |
| 3 | a-b |
a-3（
| 3 | a |
| 3 | b |
| 3 | a |
| 3 | b |
即3（
| 3 | a |
| 3 | b |
| 3 | b |
| 3 | a |
即ab（
| 3 | b |
| 3 | a |
即ab（b-a）＜0，
故选：D
点评：本题主要考查充分条件和必要条件的判断，结合不等式的性质以及立方公式是解决本题的关键．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
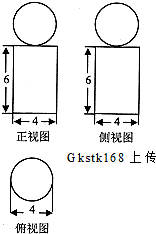如图是一个空间几何体的三视图（注：正视图也称主视图，侧视图也称左视图），其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成，俯视图是直径等于4的圆，该几何体的体积是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，写出终边落在该直线上的角的集合．
在如图所示的几何体中，四边形ABCD和ABEF均为矩形，M为AF的中点，BN⊥CE与N．