Question

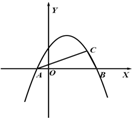如图二次函数y=ax²+

3

x+c（a＜0）的图象过点C（t，4），且与x轴相交于A，B两点，若AC⊥BC，则a的取值为（　　）

• A、-1
• B、-

  1

  4

• C、-

  1

  2

• D、-4

Answer 1

考点：二次函数的性质

专题：函数的性质及应用

分析：通过根与系数的关系得x₁+x₂，x₁x₂，再由射影定理得出等式，解出即可．

解答： 解：当b²-4ac＞0时，抛物线与x轴交于A（x₁，0），B（x₂，0），
且x₁+x₂=-

b

a

，x₁x₂=

c

a

，
过C作CD⊥x轴于D，AC⊥BC，
所以CD²=AD•BD，AD=t-x₁，BD=x₂-t，
所以4²=-（x₁x₂）+（x₁+x₂）t-t²=-

c

a

-

b

a

t-t²．
即16a=-（at²+bt+c），因为C（t，4）是抛物线上的点
，所以at²+bt+c=4，
所以a=-

1

4

．
故选：B．

点评：本题考察了韦达定理，射影定理，是一道基础题．