题目内容
已知抛物线C:y=
x2,则以抛物线的焦点F为一个焦点,且离心率为
的双曲线E的标准方程为( )
| 1 |
| 8 |
| 2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由题意可得,双曲线的一个焦点为(0,2),再根据离心率为
,求得a的值,从而可得b2的值,从而得到双曲线E的标准方程.
| 2 |
解答:
解:抛物线C:y=
x2,即x2=8y,此抛物线的焦点F(0,2),故双曲线的一个焦点为(0,2).
故对于双曲线,c=2,再根据离心率为
,可得
=
,∴a=
,∴b2=c2-a2=2,
故要求的双曲线E的标准方程
-
=1,
故选:B.
| 1 |
| 8 |
故对于双曲线,c=2,再根据离心率为
| 2 |
| 2 |
| a |
| 2 |
| 2 |
故要求的双曲线E的标准方程
| y2 |
| 2 |
| x2 |
| 2 |
故选:B.
点评:本题主要考查抛物线、双曲线的定义、性质和标准方程,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知a∈R,i为虚数单位,且复数
+
是实数,则a=( )
| a |
| 1+i |
| 1+i |
| 2 |
| A、1 | ||
B、
| ||
C、-
| ||
D、
|
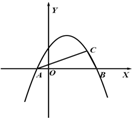 如图二次函数y=ax2+
如图二次函数y=ax2+| 3 |
| A、-1 | ||
B、-
| ||
C、-
| ||
| D、-4 |
设α角的终边上一点P的坐标是(cos
,sin
),则α等于( )
| π |
| 5 |
| π |
| 5 |
A、
| ||
B、-
| ||
C、2kπ+
| ||
D、2kπ+
|
从8名学生中,男生选2人,女生选1人,分别参加语、数、英三科比赛,共有90种不同方案,那么男、女生人数是( )
| A、2男6女 | B、6男2女 |
| C、5男3女 | D、3男5女 |
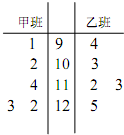 为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图:
为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图: