题目内容
复数z=
(i是虚数单位),则z的共轭复数为( )
| 1 |
| 1+i3 |
| A、1-i | ||||
| B、1+i | ||||
C、
| ||||
D、
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的运算法则和共轭复数的意义即可得出.
解答:
解:复数z=
=
=
=
=
+
i,
∴
=
-
i.
故选:D.
| 1 |
| 1+i3 |
| 1 |
| 1-i |
| 1+i |
| (1-i)(1+i) |
| 1+i |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
. |
| z |
| 1 |
| 2 |
| 1 |
| 2 |
故选:D.
点评:本题考查了复数的运算法则和共轭复数的意义,属于基础题.

练习册系列答案
相关题目
设z=1+i(i是虚数单位),则
+
=( )
| 2 |
| z |
. |
| z |
| A、2 | B、2+i |
| C、2-i | D、2-2i |
已知a∈R,i为虚数单位,且复数
+
是实数,则a=( )
| a |
| 1+i |
| 1+i |
| 2 |
| A、1 | ||
B、
| ||
C、-
| ||
D、
|
关于二项式(x-1)23有下列命题:
①该二项展开式中非常数项的系数和是1;
②该二项展开式中第六项为
x6;
③该二项展开式中系数最大的项是第13项;
④当x=24时,(x-1)23除以24的余数是23.
其中正确命题有( )
①该二项展开式中非常数项的系数和是1;
②该二项展开式中第六项为
| C | 6 23 |
③该二项展开式中系数最大的项是第13项;
④当x=24时,(x-1)23除以24的余数是23.
其中正确命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
在平面直角坐标系中,定义d(P,Q)=|x1-x2|+|y1-y2|为点P(x1,y1),Q(x2,y2)两点之间的“折线距离”,则椭圆
+y2=1上的一点P与直线3x+4y-12=0上一点Q的“折线距离”的最小值为( )
| x2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从4部甲型和5部乙型手机中任意取出3部,其中至少要有甲型与乙型手机各1部,则不同的取法共有( )
| A、35种 | B、70种 |
| C、84种 | D、140种 |
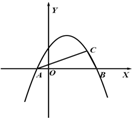 如图二次函数y=ax2+
如图二次函数y=ax2+| 3 |
| A、-1 | ||
B、-
| ||
C、-
| ||
| D、-4 |