题目内容
设数列{an}是以2为首项，1为公差的等差数列，{bn}是以1为首项，2为公比的等比数列，则ba1+ba2+…+ba6等于（ ）
| A、78 | B、84 |
| C、124 | D、126 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：根据等比数列和等差数列的通项公式，即可得到结论．
解答：
解：∵数列{an}是以2为首项，1为公差的等差数列，
∴an=2+n-1=n+1，
∵{bn}是以1为首项，2为公比的等比数列，
∴bn=2n-1，ban=2an-1=2n，
即ba1+ba2+…+ba6=2+22+…+26=126，
故选：D．
∴an=2+n-1=n+1，
∵{bn}是以1为首项，2为公比的等比数列，
∴bn=2n-1，ban=2an-1=2n，
即ba1+ba2+…+ba6=2+22+…+26=126，
故选：D．
点评：本题主要考查等差数列和等比数列的通项公式的计算，要求熟练掌握等差数列和等比数列的通项公式．
练习册系列答案
相关题目
f（x）=
x3+
x2+tanθ，则f′（1）的取值范围（ ）
| sinθ |
| 3 |
| ||
| 2 |
| A、[-2，0] |
| B、[-2，2] |
| C、[0，2] |
| D、[-1，1] |
在平面直角坐标系中，定义d（P，Q）=|x1-x2|+|y1-y2|为点P（x1，y1），Q（x2，y2）两点之间的“折线距离”，则椭圆
+y2=1上的一点P与直线3x+4y-12=0上一点Q的“折线距离”的最小值为（ ）
| x2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
向量
=（m，1），
=（n，1），则m=n是
∥
的（ ）
| a |
| b |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
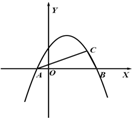如图二次函数y=ax2+| 3 |
| A、-1 | ||
B、-
| ||
C、-
| ||
| D、-4 |
函数f（x）=log2
，等比数列{an}中，a2•a5•a8=8，f（a1）+f（a2）+…+f（a9）=（ ）
| x |
| 4 |
| A、-9 | B、-8 | C、-7 | D、-10 |
设α角的终边上一点P的坐标是（cos
，sin
），则α等于（ ）
| π |
| 5 |
| π |
| 5 |
A、
| ||
B、-
| ||
C、2kπ+
| ||
D、2kπ+
|
从8名学生中，男生选2人，女生选1人，分别参加语、数、英三科比赛，共有90种不同方案，那么男、女生人数是（ ）
| A、2男6女 | B、6男2女 |
| C、5男3女 | D、3男5女 |