题目内容
已知a是实数，若（1+i）（3-ai）是纯虚数，则a=（ ）
| A、-1 | B、1 | C、-3 | D、3 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用复数的运算法则和纯虚数的意义即可得出．
解答：
解：∵复数z=（1+i）（3-ai）=3+a+（3-a）i为纯虚数，
∴
，解得a=-3．
故选：C．
∴
|
故选：C．
点评：本题考查了复数的运算法则和纯虚数的意义，属于基础题．
练习册系列答案
相关题目
设z=1+i（i是虚数单位），则
+
=（ ）
| 2 |
| z |
. |
| z |
| A、2 | B、2+i |
| C、2-i | D、2-2i |
从4部甲型和5部乙型手机中任意取出3部，其中至少要有甲型与乙型手机各1部，则不同的取法共有（ ）
| A、35种 | B、70种 |
| C、84种 | D、140种 |
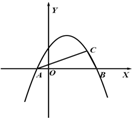如图二次函数y=ax2+| 3 |
| A、-1 | ||
B、-
| ||
C、-
| ||
| D、-4 |
已知一个空间几何体的三视图如图所示，其中俯视图是边长为6的正三角形，若这个空间几何体存在唯一的一个内切球（与该几何体各个面都相切），则这个几何体的全面积是（ ）A、18
| ||
B、36
| ||
C、45
| ||
D、54
|
设α角的终边上一点P的坐标是（cos
，sin
），则α等于（ ）
| π |
| 5 |
| π |
| 5 |
A、
| ||
B、-
| ||
C、2kπ+
| ||
D、2kπ+
|
如图，点A是单位圆与x轴正半轴的交点，点B（-