题目内容
函数f(x)=sin(ωx-
)(ω>0)的周期是π,将函数f(x)的图象沿x轴向左平移
得到函数g(x)的图象,则函数g(x)的解析式是( )
| π |
| 3 |
| π |
| 6 |
A、g(x)=sin(
| ||||
B、g(x)=sin(2x-
| ||||
| C、g(x)=sin2x | ||||
D、g(x)=sin(2x-
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:根据函数f(x)=sin(ωx-
)(ω>0)的周期是π,求得ω,再根据y=Asin(ωx+φ)的图象变换规律,求得函数g(x)的解析式.
| π |
| 3 |
解答:
解:∵函数f(x)=sin(ωx-
)(ω>0)的周期是π,
∴
=π,∴ω=2.
将函数f(x)=sin(2x-
)的图象沿x轴向左平移
得到函数g(x)=sin[2(x+
)-
]=sin2x的图象,
则函数g(x)的解析式为 g(x)=sin2x,
故选:C.
| π |
| 3 |
∴
| 2π |
| ω |
将函数f(x)=sin(2x-
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
则函数g(x)的解析式为 g(x)=sin2x,
故选:C.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知a∈R,i为虚数单位,且复数
+
是实数,则a=( )
| a |
| 1+i |
| 1+i |
| 2 |
| A、1 | ||
B、
| ||
C、-
| ||
D、
|
在平面直角坐标系中,定义d(P,Q)=|x1-x2|+|y1-y2|为点P(x1,y1),Q(x2,y2)两点之间的“折线距离”,则椭圆
+y2=1上的一点P与直线3x+4y-12=0上一点Q的“折线距离”的最小值为( )
| x2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从4部甲型和5部乙型手机中任意取出3部,其中至少要有甲型与乙型手机各1部,则不同的取法共有( )
| A、35种 | B、70种 |
| C、84种 | D、140种 |
向量
=(m,1),
=(n,1),则m=n是
∥
的( )
| a |
| b |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
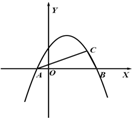 如图二次函数y=ax2+
如图二次函数y=ax2+| 3 |
| A、-1 | ||
B、-
| ||
C、-
| ||
| D、-4 |
设α角的终边上一点P的坐标是(cos
,sin
),则α等于( )
| π |
| 5 |
| π |
| 5 |
A、
| ||
B、-
| ||
C、2kπ+
| ||
D、2kπ+
|
 如图,圆O的半径为1,△ABC为圆O的内接正三角形,DA与圆O相切于点A,BD过圆心O且与圆相交于点E,则DE长为
如图,圆O的半径为1,△ABC为圆O的内接正三角形,DA与圆O相切于点A,BD过圆心O且与圆相交于点E,则DE长为