题目内容
设函数f(x)=lnx-ax+
-1.
(1)当0<a<
时,求函数f(x)的单调区间.
(2)当a=
时设函数g(x)=x2-2bx-
若对于?x1∈(0,e],?x2∈[0,1],使得f(x1)≥g(x2)成立,求实数b的取值范围(e是自然对数的底,e<
+1).
| 1-a |
| x |
(1)当0<a<
| 1 |
| 2 |
(2)当a=
| 1 |
| 3 |
| 5 |
| 12 |
| 3 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:综合题,函数的性质及应用,导数的综合应用
分析:(1)确定函数f(x)的定义域,求导函数,令f'(x)<0,可得函数f(x)的单调递减区间;令f'(x)>0,可得函数f(x)的单调递增区间,注意a的范围;
(2)当a=
时,求得函数f(x)在(0,e]上的最小值,对于?x1∈(0,e],?x2∈[0,1]使f(x1)≥g(x2)成立,等价于g(x)在[0,1]上的最小值不大于f(x)在(0,e]上的最小值,求出g(x),x∈[0,1]的最小值,即可求得b的取值范围.
(2)当a=
| 1 |
| 3 |
解答:
解:函数f(x)的定义域为(0,+∞),
(1)f(x)=lnx-ax+
-1(x>0),f′(x)=
-a+
=
(x>0),
令h(x)=ax2-x+1-a(x>0),
当a≠0时,由f′(x)=0,即ax2-x+1-a=0,解得x1=1,x2=
-1.
当0<a<
时,
-1>1>0,x∈(0,1)时,h(x)>0,f′(x)<0,函数f(x)单调递减;
x∈(1,
-1)时,h(x)<0,f′(x)>0,函数f(x)单调递增;
x∈(
-1,+∞)时,h(x)>0,f′(x)<0,函数f(x)单调递减.
综上所述:当0<a<
时,函数f(x)在(0,1)单调递减,(1,
-1)单调递增,(
-1,+∞)单调递减.
(2)当a=
时,由(1)可知函数f(x)在(0,1)上为减函数,(1,2)上为增函数,(2,e]上为减函数,
∴函数f(x)在(0,e]上的最小值为min{f(1),f(e)},而f(1)=-
,f(e)=
,且f(1)<f(e),
∴f(x)min=f(1)=-
,
若对于?x1∈(0,e],?x2∈[0,1],使得f(x1)≥g(x2)成立,等价于g(x)在[0,1]上的最小值不大于f(x)在(0,e]上的最小值(*),
又g(x)=x2-2bx-
,x∈[0,1],
①当b<0时,g(x)在[0,1]上为增函数,g(x)min=g(0)=-
>-
,与(*)矛盾;
②当0≤b≤1时,g(x)min=g(b)=-b2-
,由-b2-
≤-
及0≤b≤1,解得
≤b≤1;
③当b>1时,g(x)在[0,1]上为减函数,g(x)min=g(1)=
-2b,由
-2b≤-
及b>1,解得b>1;
综上,b的取值范围是b≥
.
(1)f(x)=lnx-ax+
| 1-a |
| x |
| 1 |
| x |
| a-1 |
| x2 |
| -ax2+x+a-1 |
| x2 |
令h(x)=ax2-x+1-a(x>0),
当a≠0时,由f′(x)=0,即ax2-x+1-a=0,解得x1=1,x2=
| 1 |
| a |
当0<a<
| 1 |
| 2 |
| 1 |
| a |
x∈(1,
| 1 |
| a |
x∈(
| 1 |
| a |
综上所述:当0<a<
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
(2)当a=
| 1 |
| 3 |
∴函数f(x)在(0,e]上的最小值为min{f(1),f(e)},而f(1)=-
| 2 |
| 3 |
| 2-e2 |
| 3e |
∴f(x)min=f(1)=-
| 2 |
| 3 |
若对于?x1∈(0,e],?x2∈[0,1],使得f(x1)≥g(x2)成立,等价于g(x)在[0,1]上的最小值不大于f(x)在(0,e]上的最小值(*),
又g(x)=x2-2bx-
| 5 |
| 12 |
①当b<0时,g(x)在[0,1]上为增函数,g(x)min=g(0)=-
| 5 |
| 12 |
| 2 |
| 3 |
②当0≤b≤1时,g(x)min=g(b)=-b2-
| 5 |
| 12 |
| 5 |
| 12 |
| 2 |
| 3 |
| 1 |
| 2 |
③当b>1时,g(x)在[0,1]上为减函数,g(x)min=g(1)=
| 7 |
| 12 |
| 7 |
| 12 |
| 2 |
| 3 |
综上,b的取值范围是b≥
| 1 |
| 2 |
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查转化思想、分类讨论思想,解题的关键是将对于?x1∈(0,e],?x2∈[0,1],使得f(x1)≥g(x2)成立,等价于g(x)在[0,1]上的最小值不大于f(x)在(0,e]上的最小值.

练习册系列答案
相关题目
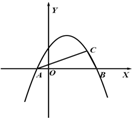 如图二次函数y=ax2+
如图二次函数y=ax2+| 3 |
| A、-1 | ||
B、-
| ||
C、-
| ||
| D、-4 |
 如图,△ABC的三个内角分别为A,B,C,cosA=
如图,△ABC的三个内角分别为A,B,C,cosA= 如图,点A是单位圆与x轴正半轴的交点,点B(-
如图,点A是单位圆与x轴正半轴的交点,点B(-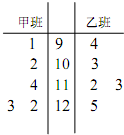 为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图:
为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图: