题目内容
9.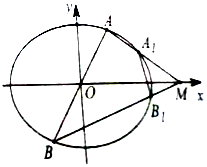 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,焦距为2,直线y=kx(x≠0)与椭圆C交于A,B两点,M为其右准线与x轴的交点,直线AM,BM分别与椭圆C交于A1,B1两点,记直线A1B1的斜率为k1
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,焦距为2,直线y=kx(x≠0)与椭圆C交于A,B两点,M为其右准线与x轴的交点,直线AM,BM分别与椭圆C交于A1,B1两点,记直线A1B1的斜率为k1(1)求椭圆C的方程;
(2)是否存在常数λ,使得k1=λk恒成立?若存在,求出λ的值;若不存在,请说明理由.
分析 (1)由题意c=1,根据椭圆的离心率,即可求得a的值,b2=a2-c2=1,即可求得椭圆方程;
(2)根据椭圆的准线方程,即可求得AM的方程,代入椭圆方程,利用韦达定理即可求得A1及B1,k1=$\frac{-6{y}_{0}}{2{x}_{0}}$=-3k,存在λ=-3,使得k1=λk恒成立.
解答 解:(1)由椭圆的焦距2c=2,则c=1,双曲线的离心率e=$\frac{c}{a}$=$\frac{{\sqrt{2}}}{2}$,则a=$\sqrt{2}$,
则b2=a2-c2=1,
∴椭圆的标准方程:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)设A(x0,y0),则2y02=2-y02,则B(-x0,-y0),k=$\frac{{y}_{0}}{{x}_{0}}$,
右准线方程x=2,则M(2,0),
直线AM的方程为y=$\frac{{y}_{0}}{{x}_{0}-2}$(x-2),
$\left\{\begin{array}{l}{y=\frac{{y}_{0}}{{x}_{0}-2}(x-2)}\\{\frac{{x}^{2}}{2}+{y}^{2}=2}\end{array}\right.$,整理得:(x0-2)2x2+2y02(x-2)2-2(x0-2)2=0,
该方程两个根为x0,${x}_{{A}_{1}}$,
∴x0•${x}_{{A}_{1}}$=$\frac{8{y}_{0}^{2}-2({x}_{0}-2)^{2}}{({x}_{0}-2)^{2}+2{y}_{0}^{2}}$=$\frac{4(2-{x}_{0}^{2})-2({x}_{0}-2)^{2}}{({x}_{0}-2)^{2}+2-{x}_{0}^{2}}$=$\frac{4-3{x}_{0}}{3-2{x}_{0}}$•x0,
则${x}_{{A}_{1}}$=$\frac{4-3{x}_{0}}{3-2{x}_{0}}$,${y}_{{A}_{1}}$=$\frac{{y}_{0}}{{x}_{0}-2}$(${x}_{{A}_{1}}$-2)=$\frac{{y}_{0}}{3-2{x}_{0}}$,
则A1($\frac{4-3{x}_{0}}{3-2{x}_{0}}$,$\frac{{y}_{0}}{3-2{x}_{0}}$),同理可得B1($\frac{4+3{x}_{0}}{3+2{x}_{0}}$,-$\frac{{y}_{0}}{3+2{x}_{0}}$),
则k1=$\frac{-6{y}_{0}}{2{x}_{0}}$=-3k,
即存在λ=-3,使得k1=λk恒成立.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,考查计算能力,属于中档题.


| A. | $\frac{4}{3}$ | B. | 2 | C. | $\frac{8}{3}$ | D. | 4 |
 《孙子算经》中有道算术题:“今有百鹿人城,家取一鹿不尽,又三
《孙子算经》中有道算术题:“今有百鹿人城,家取一鹿不尽,又三家共一鹿适尽,问城中家几何?”意思是有100头鹿,每户分1头还有
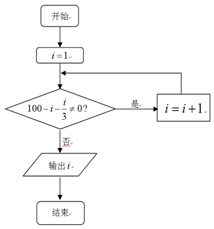
剩余;再每3户共分1头,正好分完,问共有多少户人家?设计框图如
下,则输出的值是( )
| A. | 74 | B. | 75 | C. | 76 | D. | 77 |
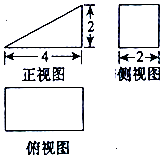
| A. | $20+4\sqrt{5}$ | B. | $12+4\sqrt{5}$ | C. | $20+2\sqrt{5}$ | D. | $12+2\sqrt{5}$ |
| A. | (-∞,-3)∪(0,3) | B. | (-2,0)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(3,+∞) |
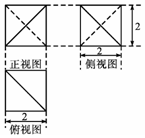 如图是某多面体的三视图,则该几何体的外接球体积为4$\sqrt{3}$π.
如图是某多面体的三视图,则该几何体的外接球体积为4$\sqrt{3}$π.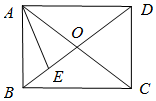 在矩形ABCD中,对角线AC,BD相交于点O,E为BO的中点,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ为实数),则λμ=$\frac{3}{16}$.
在矩形ABCD中,对角线AC,BD相交于点O,E为BO的中点,若$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AD}$(λ,μ为实数),则λμ=$\frac{3}{16}$.