题目内容
已知（1+i）（1-mi）=2i（i是虚数单位），则实数m的值为（ ）
| A、±1 | B、1 | C、2 | D、-1 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：由复数代数形式的乘除运算化简等式左边为a+bi（a，b∈R）的形式，再由复数相等的条件列式求得实数m的值．
解答：
解：∵（1+i）（1-mi）=1-mi+i-mi2=（1+m）+（1-m）i，
由（1+i）（1-mi）=2i，
得
，
解得m=-1．
故选：D．
由（1+i）（1-mi）=2i，
得
|
解得m=-1．
故选：D．
点评：本题考查了复数代数形式的乘除运算，考查了复数相等的条件，是基础的计算题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
在△ABC中，若
=1，则∠C的大小为（ ）
| c2-a2 |
| b2+ab |
A、
| ||
B、
| ||
C、
| ||
D、
|
若在△ABC中，有sin
=cosA，则△ABC一定是（ ）
| C |
| 2 |
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、等腰三角形 |
对于任意x∈[-1，0]，恒有
x3-x2-3x-2m≤3成立，则m的取值范围为（ ）
| 1 |
| 3 |
A、[-
| ||
| B、[-1，+∞） | ||
C、[-
| ||
| D、[-2，+∞） |
设平面向量
，
，
均为非零向量，则“
•（
-
）=0”是“
=
”的（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
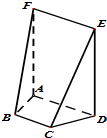如图，在五面体ABCDEF中，四边形ADEF是正方形，FA⊥面ABCD，BC∥AD，CD=1，AD=