题目内容
不等式
≤1的解集是( )
| 4 |
| x+1 |
| A、(-∞,-1]∪(3,+∞) |
| B、(-1,3] |
| C、[-1,3] |
| D、(-∞,-1)∪[3,+∞) |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:依题意,作差可得
≤0,再转化为不等式组
①或
②,分别解之,再取并即可.
| 3-x |
| x+1 |
|
|
解答:
解:∵
-1=
≤0,
∴
①或
②,
解①得:x≥3;
解②得:x<-1,
∴不等式
≤1的解集是(-∞,-1]∪[3,+∞),
故选:D.
| 4 |
| x+1 |
| 3-x |
| x+1 |
∴
|
|
解①得:x≥3;
解②得:x<-1,
∴不等式
| 4 |
| x+1 |
故选:D.
点评:本题考查分式不等式的解法,等价转化为为一次不等式组是关键,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知某几何体的三视图如图所示,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )
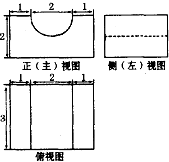

A、24-
| ||
B、24-
| ||
| C、24-π | ||
D、24-
|
已知定义在R上的奇函数f(x),且为减函数,又知f(1-a)+f(1-a2)<0,则a的取值范围为( )
| A、(-2,1) |
| B、(-∞,-2)∪(1,+∞) |
| C、(0,1) |
| D、(0,2) |
在△ABC中,若(a+c)(a-c)=b(b-c),则∠A=( )
| A、90° | B、60° |
| C、120° | D、150° |
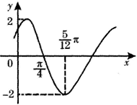 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<