Question

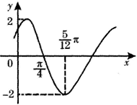已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜

π

2

）的图象如图，则f（x）的解析式为

 

．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的求值,三角函数的图像与性质

分析：首先利用函数的最值确定A的值，进一步利用周期公式确定ω，最后利用x=

π

4

时，f(

π

4

)=0求出φ的值，进一步求出函数的解析式．

解答： 解：函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜

π

2

）的图象如图函数的最大值和最小值为：±2
所以：A=2

T

4

=

5π

12

-

π

4

解得：T=

2π

3

所以：ω=

2π

T

=3
当x=

π

4

时，f(

π

4

)=0）
由于：|φ|＜

π

2

所以：φ=

π

4

所以：f(x)=2sin(3x+

π

4

)
故答案为：f(x)=2sin(3x+

π

4

)

点评：本题考查的知识要点：利用函数的图象求正弦型函数的解析式，主要确定A、ω和φ的值．