题目内容
在△ABC中，若（a+c）（a-c）=b（b-c），则∠A=（ ）
| A、90° | B、60° |
| C、120° | D、150° |
考点：余弦定理
专题：解三角形
分析：利用余弦定理表示出cosA，把已知等式代入计算求出cosA的值，即可确定出A的度数．
解答：
解：∵在△ABC中，（a+c）（a-c）=b（b-c），即c2+b2-a2=bc，
∴cosA=
=
=
，
则A=60°，
故选：B．
∴cosA=
| c2+b2-a2 |
| 2bc |
| bc |
| 2bc |
| 1 |
| 2 |
则A=60°，
故选：B．
点评：此题考查了余弦定理，熟练掌握余弦定理是解本题的关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
相关题目
不等式
≤1的解集是（ ）
| 4 |
| x+1 |
| A、（-∞，-1]∪（3，+∞） |
| B、（-1，3] |
| C、[-1，3] |
| D、（-∞，-1）∪[3，+∞） |
已知角α的终边经过点（3，-4），则tan
=（ ）
| α |
| 2 |
A、-
| ||
B、-
| ||
| C、2 | ||
| D、3 |
等差数列{an}的前3项和为30，前6项和为100，则它的前9项和是（ ）
| A、130 | B、170 |
| C、210 | D、260 |
已知集合A={2，3，4，5}，B={3，5，6}，则A∩B=（ ）
| A、{3} |
| B、{2，4} |
| C、{2，3，4，5，6} |
| D、{3，5} |
设a=lg3，b=（lg3）2，c=lg
，则有（ ）
| 3 |
| A、a＞c＞b |
| B、a＞b＞c |
| C、b＞c＞a |
| D、b＞a＞c |
设0＜a＜1，m=loga(a2+1)，n=loga（a+1），p=logaa，则m，n，p的大小关系是（ ）
| A、n＞m＞p |
| B、m＞p＞n |
| C、m＞n＞p |
| D、p＞m＞n |
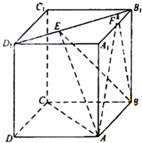如图，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=1，则下列结论中正确的有