题目内容
已知定义在R上的奇函数f(x),且为减函数,又知f(1-a)+f(1-a2)<0,则a的取值范围为( )
| A、(-2,1) |
| B、(-∞,-2)∪(1,+∞) |
| C、(0,1) |
| D、(0,2) |
考点:函数奇偶性的性质,函数单调性的性质
专题:函数的性质及应用
分析:本题由于已知函数为奇函数,所以f(-x)=-f(x),而f(1-a)+f(1-a2)<0得到f(1-a)<-f(1-a2)=f(a2-1),根据函数的单调递减可知,1-a>a2-1,求出解集得到本题结论.
解答:
解:∵函数y=f(x)为奇函数,
∴f(-x)=-f(x),
∵f(1-a)+f(1-a2)<0,
∴f(1-a)<-f(1-a2)=f(a2-1),
∵f(x)在R的奇函数f(x),在[0,+∞)上单调递减,
由奇函数的对称性可知,f(x)在R上单调递减,
∴根据函数单调递减可知1-a>a2-1,
∴a2+a-2<0,
解得a<-2或a>1,
故选:B.
∴f(-x)=-f(x),
∵f(1-a)+f(1-a2)<0,
∴f(1-a)<-f(1-a2)=f(a2-1),
∵f(x)在R的奇函数f(x),在[0,+∞)上单调递减,
由奇函数的对称性可知,f(x)在R上单调递减,
∴根据函数单调递减可知1-a>a2-1,
∴a2+a-2<0,
解得a<-2或a>1,
故选:B.
点评:本题主要考查了函数的奇偶性、单调性在解决抽象不等式中的应用,灵活应用函数知识是解答本题的关键,本题难度不大,属于基础题.

练习册系列答案
相关题目
点P在直线x+y-4=0上,O为原点,则|OP|的最小值是( )
| A、2 | ||
B、
| ||
C、2
| ||
D、
|
已知△ABC的内角A,B,C所对应的边分别为a,b,c,若cosC>
,则△ABC的形状是( )
| b |
| a |
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、钝角三角形 |
不等式
≤1的解集是( )
| 4 |
| x+1 |
| A、(-∞,-1]∪(3,+∞) |
| B、(-1,3] |
| C、[-1,3] |
| D、(-∞,-1)∪[3,+∞) |
公比为q的等比数列{an}的各项为正数,且a2a12=16,logqa10=7,则公比q=( )
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
(文)长度为6的动弦AB在抛物线y2=4x上滑动,AB中点到y轴距离的最小值为2,则直线AB的斜率为( )
| A、± | ||
B、±
| ||
C、±
| ||
| D、±2 |
设a=lg3,b=(lg3)2,c=lg
,则有( )
| 3 |
| A、a>c>b |
| B、a>b>c |
| C、b>c>a |
| D、b>a>c |
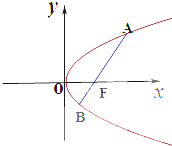 如图,给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点
如图,给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点